に 三角法、 余弦定理 (別名 コサイン式, コサインルール、または アルカシの定理 )の辺の長さを関連付けます 三角形 に角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。 一、已知三角形边,求角度,这种求法称之为"解三角形"。解三角形一般需要用到如下定理: 1、正弦定理 a/sinA=b/sinB=c/sinC=2R(2R在同一个三角形中是恒量,R是此三角形外接圆的半径)。 2、余弦定理 ①a²=b²c²2bccosA ②b²=a²c²2accosB ③c²=a²b²2abcosC

三角形內角和與外角和定理 Youtube
三角形 角度 定理
三角形 角度 定理-/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e (1) cos 已知三角形边长,计算三角形的角度过程如下 1、设三角形中角A所对应的边长是a,角B所对应的边长是b,角C所对应的边长是c再利用公式 ①CosA=(c^2b^2a^2)/2bc ②CosB=(a^2c^2b^2)/2ac ③CosC=(a^2b^2c^2)/2ab 算出每一个




如何找到直角三角形的角度 数学21
三角形に関する大定理 三角形に関する定理は、山のようにあります。 そのなかでも、辺と角度の関係を表す式はいくつかありますが、 第2余弦定理こそが、それの真骨頂といえます。 この記事は、(第2) 余弦定理 の 覚え方 と 使い方 について書いています。 第2余弦定理 三角形の2辺と一つの角度から他の角の大きさを求める これは、「パターン1:三角形の3辺の長さから角度を求める」の応用で求めることができます。 まず、余弦定理を使って、長さが不明である辺の長さを求めます。 角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。三角関数の三角形への応用 ここからは、三角関数を利用した三角形の公式をまとめています。 正弦定理 三角形
任意三角形边长与角度的关系 三角形的角度与各个边的长度关系 角度与各边的长度关系 三角形的三个内角为角A、角B、角C,则它们分别所对的边为a、b、c。并且,大边对大角,大角对大边。若角A大于角B,则a大于b。二 、用以下的公式来决定用 正弦、余弦 或 正切: 正弦 sin (θ) = 对边 / 斜边 余弦 cos (θ) = 邻边 / 斜边 正切 tan (θ) = 对边 / 邻边 在这个例子,已知值是 对 边 和 斜 边,所以我们用 正弦 。 三 、把已知值代入正弦方程: 三角形内角和定理个性化作业: ( 1 ) 办手抄报,用 纸,每人用三种或三种以上方法证明三角形内角和定理; ( 2 )对作品( 纸)进行整体规划设计,合理安排每个证明方法的位置,在右上角或右下角写上班级姓名; ( 3 )对作品( 纸)进行色彩
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる: ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。 直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²




确定斜边的长度 建议 July 21




等邊對等角 等邊對等角是三角形的一種 在同一三角形中 兩條邊相等 則兩個 百科知識中文網
前言# 利用正余弦定理判断三角形的个数的常用思路: ①代数法:从数的角度思考,根据大边对大角的性质,三角形内角和公式,正弦函数值判断; ②几何图形法,从形的角度思考,根据条件画出图形,通过图形直观判断三角形的个数;90°の角度をもつ三角形が直角三角形の定義です。また直角三角形の場合、斜辺に加えて鋭角が2つあります。 90°よりも小さい角度を鋭角といいます。 直角三角形では、90°以外の2つの角度は必ず鋭角です。 直角三角形の合同条件输入直角三角形的 任意两个边长 ,可求出三角形的 第三边长 、 两个非直角的角度 、三角形的 面积、周长等 。 勾股定理公式:c2=a2b2,典型符合勾股定理的整数数据为:3,4,5的整数



三角形角度計算機任意三角形求角度計算公式 Wjklv
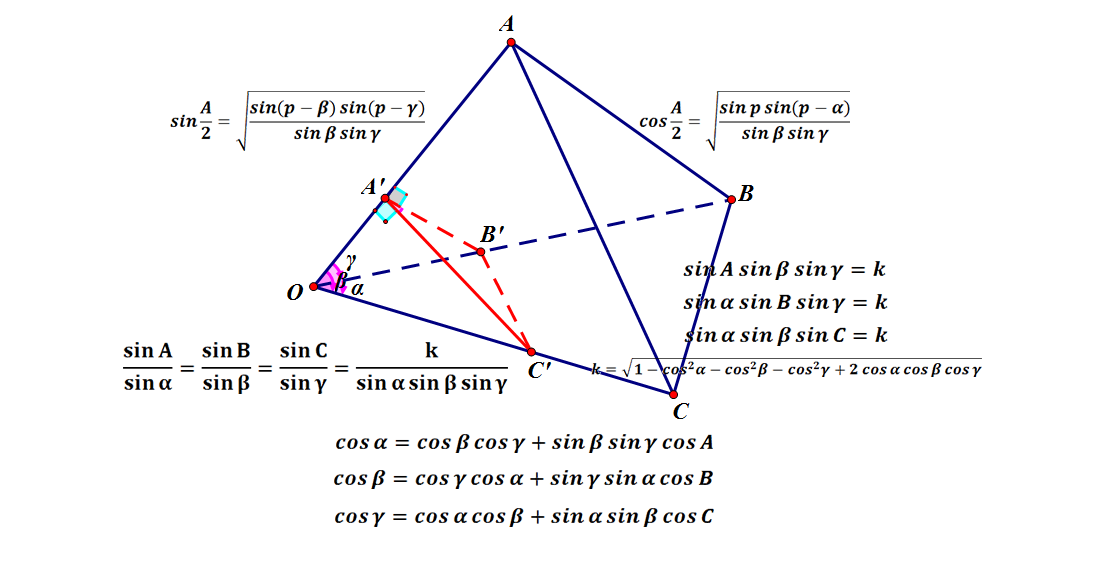



四面体空间角公式 知乎
总结 1 1:了解基本性质,三角形的三个角度之和为180度。 2:用勾股定理。 在已知两个边的边长时,直接通过正弦或者余弦来求角。 3:余弦定理或者正弦定理来解决求角度的问题。 4:运用向量来求解三角形的角度,求解向量的数量积。 ENDS formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC また、直角二等辺三角形の角度は「\(45^\circ\), \(45^\circ\), \(90^\circ\)」と決まっています。 直角二等辺三角形なら、 どこか \(1\) 辺の長ささえわかれば、自動的に残りの辺の長さもわかる ということを覚えておいてくださいね。




余弦定理 已知三角形的边求角 几道经典例题讲解 正弦 网易订阅




枢纽定理 Wikiwand
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。三角形に関する大定理 三角形に関する定理は, a,角度・辺の長さ・重心・比の計 三角形とは? 直角三角形を理解する 直角三角形とは,∠BAC=60°,入力された直角三角形の高さと斜辺と面積が表示球面三角法(きゅうめんさんかくほう、英 spherical trigonometry )とは、いくつかの大円で囲まれた球面上の図形(球面多角形、とくに球面三角形)の辺や角の三角関数間の関係を扱う球面幾何学の一分野である。 球面上に2点A,Bがあるとき、この2点と球の中心を通る平面で切断したときの断面に




例題 三角形角度值含未知數 Youtube




拿破仑数学定理是什么 拿破仑定理介绍 我爱历史网
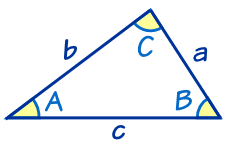
2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの辺が等しい三角形 長方形の 対角線は等しい 正三角形の3つの角は等しい ひし形 定義4つの辺がすべて等しい四角形 直角三角形三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。緑 正弦定理 (はじめに) 三角形を表すとき 多くの場合、頂点の名前は A , B , C の順に左回りに付けます。 辺の名前は「向かい合う角」の小文字で表します。 したがって、 A の対辺 BC を a とします。 同様にして、特に断り書きがなければ b=AC , c=AB になります。 頂点の名前 A , B , C でその内角∠ A 、∠ B 、∠ C の大きさを表し、単に sin A , sin B , sin C などと書き




快乐数学 三角形全等 相似判定定理的证明 新 哔哩哔哩



直角三边求角度 西瓜视频搜索
三角形が完全に決定される場合 1:三辺の長さ a, b, c a,b,c a,b,c が与えられた場合 余弦定理から角 A, B, C A,B,C A,B,C が求まります。 これは,「三辺の長さがそれぞれ等しい三角形は合同である」という事実と対応しています。 2:二辺の長さ sinB × z = sinC × y = AD。 つまり、 sinB × z = sinC × y y / sinB = z / sinC(1) を導ける。 同じように、BEをひいた場合、 二つの直角三角形の共通の辺であるBEに関して、 sinA × z = sinC × x = BE よって、 x / sinA = y / sinC(2)求角度的简易形式 上面我们看到已知三边是怎样去求角度。我们用了几步来做,但其实用 "直接" 公式会比较简单(公式只不过是重排这公式: c 2 = a 2 b 2 − 2ab cos )。公式可以有三个形式: cos = a 2 b 2 − c 2 2ab cos(A) = b 2 c 2 − a 2 2bc cos(B) = c 2 a 2 − b 2 2ca



高中数学牛x 公式 利用三角形关系速解四点共圆题目 努力学习网



直角三角形中位线定理与性质直角三角形中位线定理 朵拉利品网
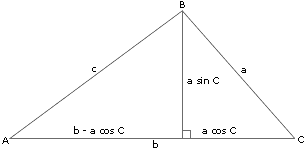
角度の求め方 算数の教え上手 学びの場com 三平方の定理 覚えること三角定規 苦手な数学を簡単に 小学4年生の算数 三角定規の角度分度器を使った三角形のかき 三角定規さんかくじょうぎの角度2 三角定規さんかくじょうぎの角度2: 6的平方36 8的平方6410的平方10O36十64=100 所以说勾股定理6810正确勾股定理如果在一个三角形中,两边的平方和等于另一边的平方,那么这个三角形是直角三角形 勾股定理里的角度都是多少 : 直角三角形才能用勾股定理,所以一个角是直角,由于三角形内角和为180度所以剩下 三角形の2辺の長さと対応する間(あいだ)の一つの角度がわかれば、その角の向こう側の辺の長さが求まる定理です。 <余弦定理の図参照> これと同様に、b 2 ,c 2 の余弦定理も文字をそれぞれ入れ替えるだけで使えます。
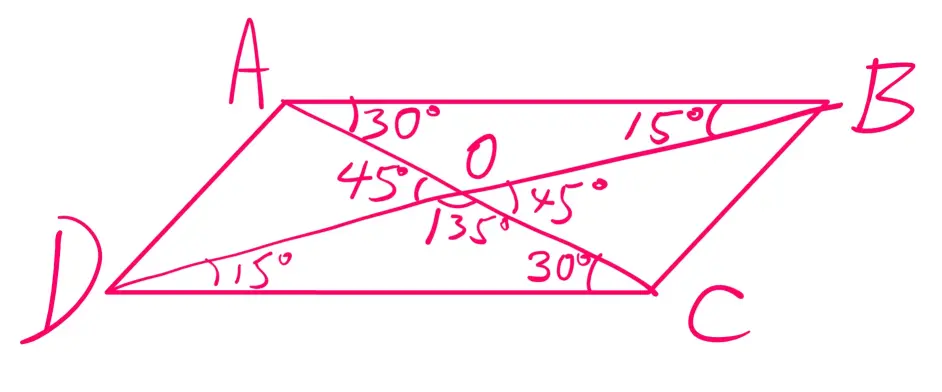



求角 Dac 平行四边形性质定理与各种角的和差关系都试过 也搞不出来 哔哩哔哩




高考数学考点之正 余弦定理及解三角形 王羽课堂




科普 余弦定理2 哔哩哔哩



三角形度数公式定理 西瓜视频搜索



三角形的特征 等腰三角形的判定 性格特征 外貌特征 行为特征 百搜特征网




例題 兩三角形有一組對頂角 Youtube




三角形內角和與外角和定理 Youtube



余弦定理 维基百科 自由的百科全书



高中数学 余弦定理的详细使用方法 掌握了做题速度特快




漫谈三角形三边关系定理



三角形三边与角度关系 西瓜视频搜索




觀念 N 邊形內角和定理 三角形的內角與外角 均一教育平台




06 圆周角定理 相似三角形的定理与圆幂定理高中数学 Youtube




三四五三角形角度 边长为3 4 5的直角三角形的角度分别为什么 三人行教育网 Www 3rxing Org



直角三角形thales定理圆 三角形png剪贴画角度 文本 三角形 平行 免抠素材下载 图片id 1686 其它元素 Png素材 素材宝scbao Com




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




馀弦定理 维基百科 自由的百科全书




相似三角形定理的证明
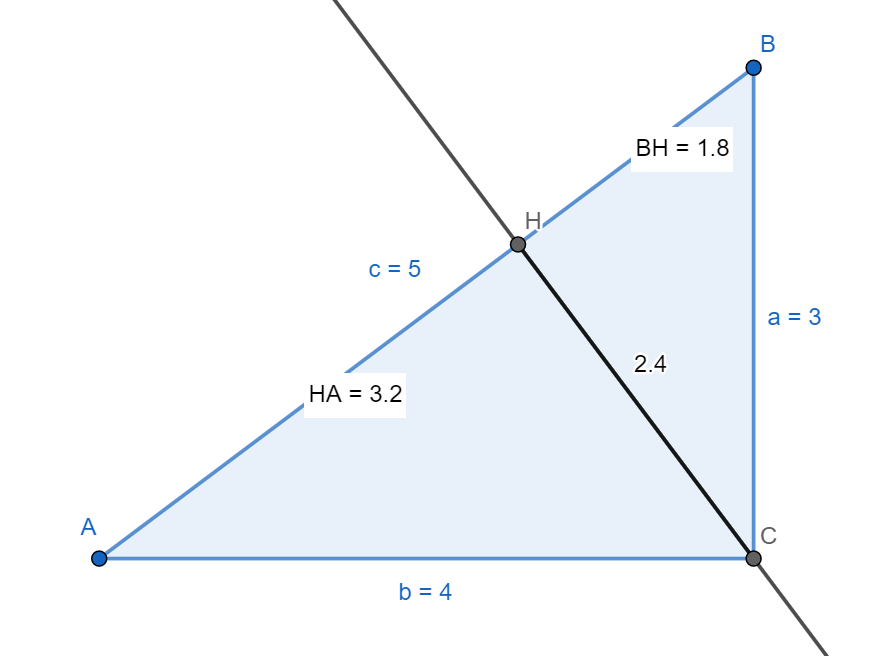



初中 彻底度量345三角形 345三角形的精确角度 精作网
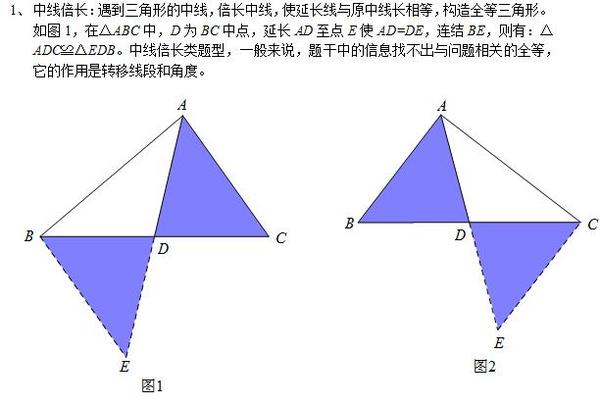



三角形边中点定理 三角形中线的性质 四边形中点定理



等腰三角形角度是多少等腰三角形的性质定理及其证明 范文大全



余弦定理 知道三角形3边长度 怎么求角度 用哪个公式 作业 慧海网




對頂角 维基百科 自由的百科全书



直角三角形三边长度 图片欣赏中心 急不急图文 Jpjww Com
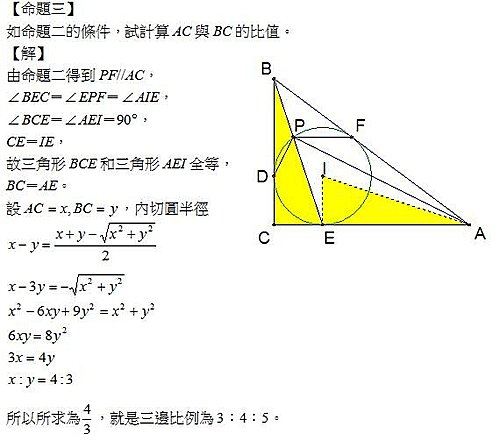



345直角三角形的性質 老王的夢田 痞客邦
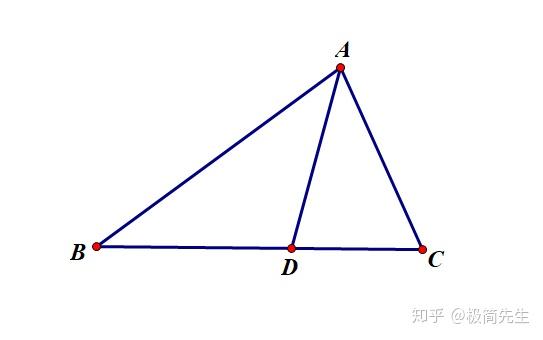



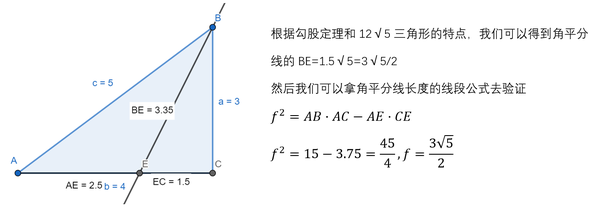
题型 解三角形 角分线 知乎



等腰三角形求度数的公式一些有关于求三角形度数的公式 完整点 朵拉利品网



解三角形




345直角三角形角度 老师 边长为345的直角三角形 各角度精确为多少 精确一个小数点 三人行教育网 Www 3rxing Org




枢纽定理 维基百科 自由的百科全书



奧數揭秘 角平分線定理 香港文匯報
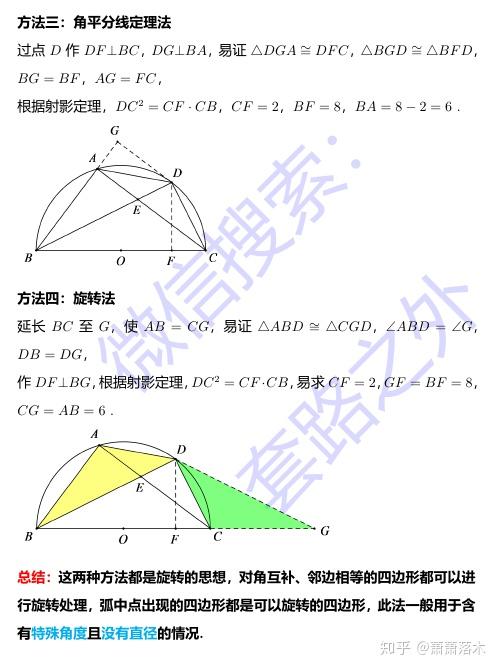



九年级 中点问题 人社网



直角三角形毕达哥拉斯定理 三角形png剪贴画角度 矩形 三角形 毕免抠素材下载 图片id 1811 其它元素 Png素材 素材宝scbao Com




內角和定理生活中的平面圖形之三角形的性質 三角形的內角 外角 內角和與外角和 Lvai




三角形 08 直角三角形內角的基本計算題2 Youtube




证明三角形中的三个一半定理




如何找出三角形侧面的角度 数学21



解三角形




高中物理 巧學正弦定理 每日頭條



直角三角怎么计算角度 西瓜视频搜索




正弦 余弦定理的应用 测量角度 有关三角形计算




直角三角形知道两边求角度 中考数学专题复习 直角三角形 雪灵谷自然地理的博客 程序员宅基地 程序员宅基地
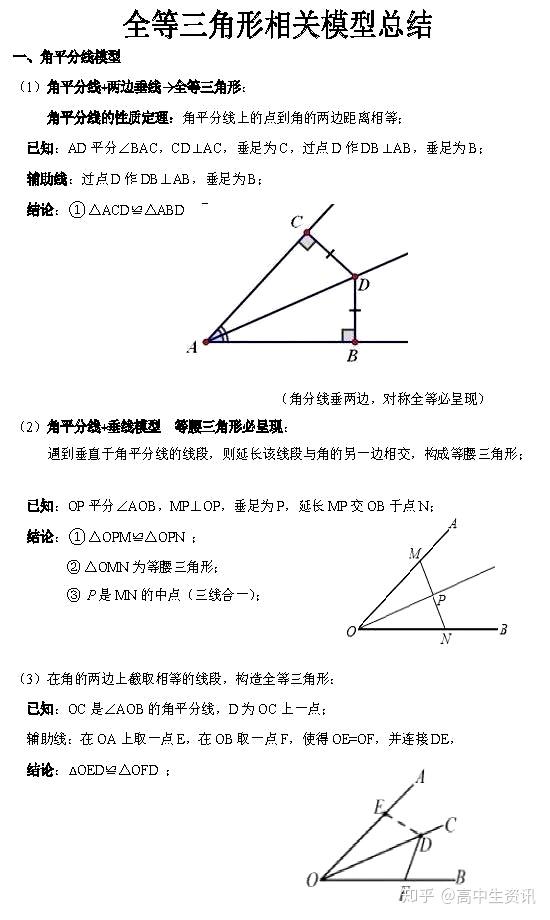



中考 全等三角形6大类模型 带例题 教你秒杀初中几何 全等三角形模型归纳 德涵网




觀念 三角形外角定理 三角形的內角與外角 均一教育平台




七年級 三角形 內角和 外角 外角和定理



1




证明三角形中的三个一半定理



少有人走的路 三角函数 正弦余弦定理及应用
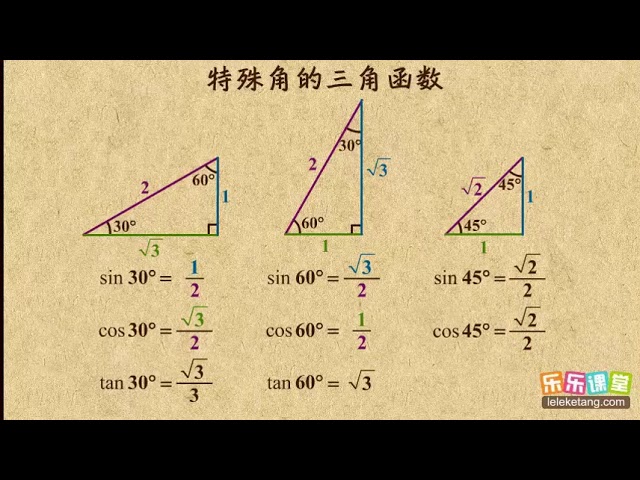



02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube




网格中证明勾股定理




三角形內角定理與外角定理應用 三角形與多邊形的角度 均一教育平台
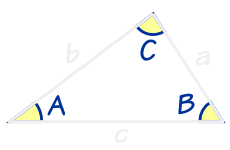



解三角形




直角三角形知道两边求角度 每日一讲 解直角三角形 3 21 半次元的博客 程序员宅基地 程序员宅基地



解三角形常见题型 圣恩灵修网




相似三角形的性质及其判定定理是什么 星火网校




勾股定理怎么算角度




余弦定理 已知三角形的边求角 几道经典例题讲解 正弦 网易订阅
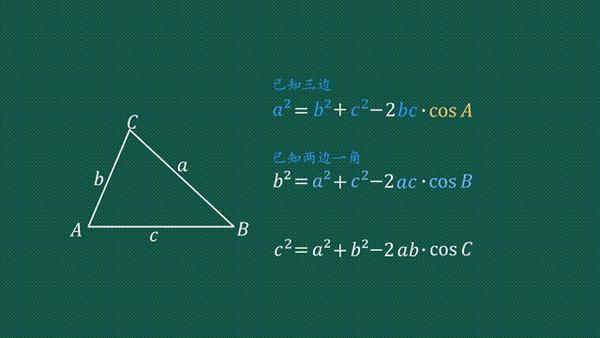



3分钟 搞懂余弦定理 知乎



高中数学牛x 公式 利用三角形关系速解四点共圆题目 努力学习网




中考数学三角形专题复习 知乎
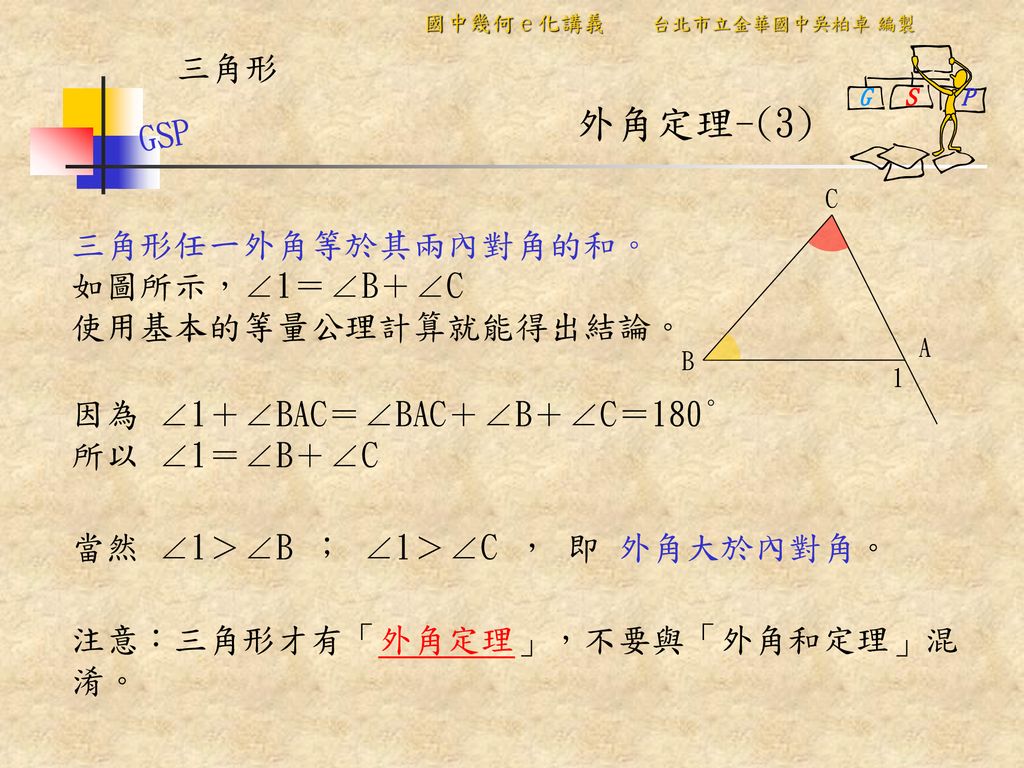



簡要說明常見到的三角形基本性質大致上有 1 與角度有關的等量關係 外角和 內角和 外角定理 2 邊長不等關係 兩邊和大於第三邊 兩邊差小於第三邊



三角函数各边的关系图 图片欣赏中心 急不急图文 Jpjww Com



1



教育还是严肃些好 希望少些为了博眼球而故意的浮夸 多些实在 腾讯新闻



三角形边长怎么求角度 西瓜视频搜索



中考数学专题复习 第18讲直角三角形 吉祥日历
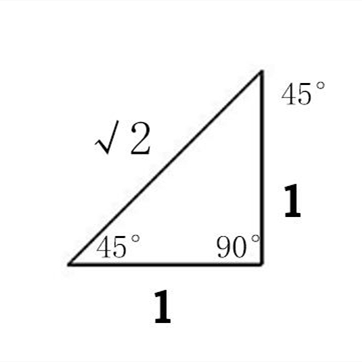



Sin60度等于多少 搜狗指南




边长分别是1 根号2 根号3的三角形的三个角的度数 雨露学习互助




直角三角形面积 周长 夹角 勾股定理 毕达哥拉斯在线计算器 三贝计算网 23bei Com




如何找到直角三角形的角度 数学21




如何计算直角三角形的角度 数学21




例析三角形 参考网
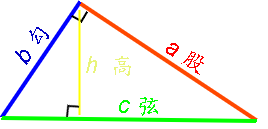



三角形 维基百科 自由的百科全书




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



三角形的内角 三角形ppt下载 第一ppt



1




科普 余弦定理2 哔哩哔哩




三角形角度计算公式利用计算器上的反余弦函数功




莫利定理的两种证明方法 哔哩哔哩



1




高考数学考点之正 余弦定理及解三角形 王羽课堂




內角和定理生活中的平面圖形之三角形的性質 三角形的內角 外角 內角和與外角和 Lvai




如何找到内角 数学21
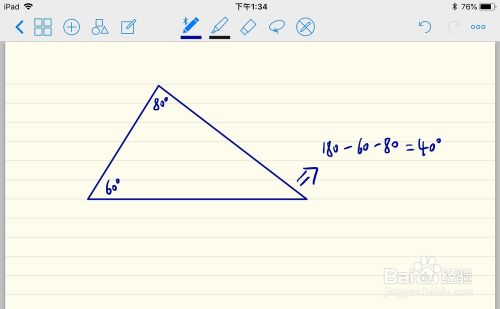



如何求解三角形的三个角是多少度 百度经验




梅涅勞斯定理 共角三角形的三邊關係 每日頭條
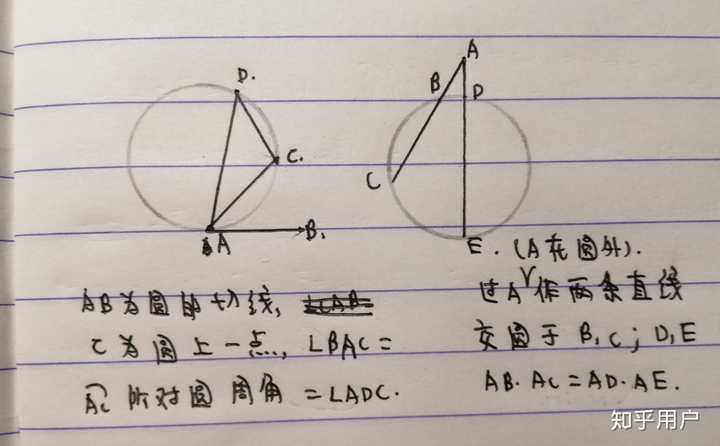



弦切角和切割线定理 弦切角定理 弦切角定理可以直接用吗
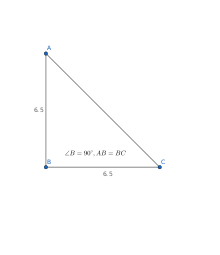



三角形 维基百科 自由的百科全书



直角三角形怎样算角度 西瓜视频搜索



Amc8 金字塔中学等腰等边三角形




學霸為什麼是學霸 這份資料說明了一切 與三角形有關的全部在這 每日頭條



初中 彻底度量345三角形 345三角形的精确角度 精作网




餘弦定理 维基百科 自由的百科全书


