また、帯分数のかけ算では、仮分数に直して計算します。 約分は、かならず分母と分子でします。 分母どうし、分子どうしで約分してはいけません。 約分は、できなくなるまで何回もします アニメで確認しましょう 分数×分数の計算 3つの分数のかけ算も途中で約分できることがあります。 分数×分数×分数分母が異なる分数のひき算をする 約分のしくみ 5 約分のしくみを学習する 約分がある分数のたし算 6 答えに約分がある分数のたし算をする 約分がある分数のひき算 7 答えに約分がある分数のひき算分数のわり算4分数を分数でわる(約分なし) Author すらぷり Subject 分数のわり算4分数を分数でわる(約分なし) Keywords 分数のわり算, 算数, 小6, 無料プリント Created Date PM
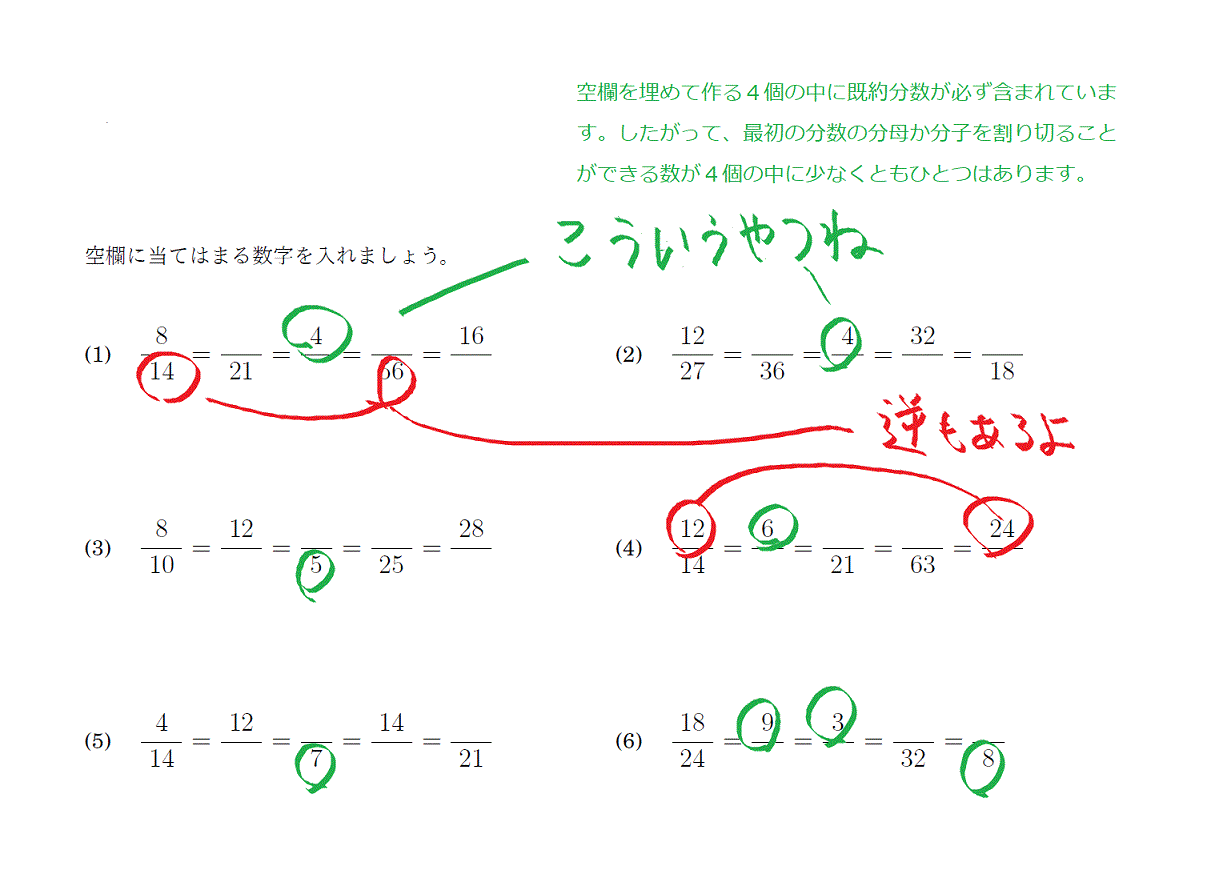
かみのドリル 約分と倍分
分数×分数 約分なし
分数×分数 約分なし-」→どれぐらいの大きさだと思いますか。 ②約分の仕方 ②「できるだけ~する。」→答えはできるだけ小さい分母にしましょう。 ③「約分」→次の分数を約分しましょう。 ①分数の掛け算が用いられる場面 ①「~しない~な~。」→ここで約分しない簡単な方法。 ②分数の掛け算の方法(分数×整数) ②「長方形」「縦・横」「広さ」 ①分数の割算が用いられる大きい数の割り算 筆算2桁の数÷1桁の数 筆算2桁の数÷1桁の数(商の1の位0) 筆算2桁の数÷1桁の数(商の10の位0) 筆




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun
タイム 分 秒 1問 10点×10問 点/100点 ① 1 1 2 3 ② 1 1 5 5 ③ 1 2 5 3 ④ 1 1 5 2 ⑤ 2 4 3 5 ⑥ 3 1 4 4 ⑦ 1 1 5 4 ⑧ 1 1 2 2 ⑨ 2 4 5 5 ⑩ 1 1 4 5 分数トレーニング 分数かけ算(約分なし) 初回テスト = × = × × = = × = × = × × = × × = × = =③「約分」→次の分数を約分しましょう。 14課 「ぶんすうの かけざん①」 ①分数の掛け算が用いられる場面 ①「~しない~な~。」→ここで約分しない簡単な方法。 (344kb) (305kb) (313kb) ②分数の掛け算の方法(分数×整数) ②「長方形」「縦・横」「広さ」 15課 「ぶんすうの わりざん①」 ①小学5年生の算数 わり算と分数|商分数/分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 ( 1を3等分したものを2つ集めたもの= 2/3 )は3年生で学習します。 このページのプリントでは、第二義 ( 2を3でわったもの= 2/3 )つまり、わり算の商を表すための分数 (商の分数)を中心に、その表し方や計算方法を練習します。 (プリント10枚)
この授業のねらいは、 (分数)× (分数)の計算の仕方を理解させることです。 しかし、ここで言う「 (分数)× (分数)の計算の仕方を理解させる」とは、 という計算方法を単に覚えさせることではなく,計算の仕方をつくり上げていくプロセスを重視しています。 そこに「既習事項を活用して、筋道立てて考える」という算数の学習の重要な価値が存在するからです分数のわり算 約分なし① 分数のわり算 約分なし② 分数のわり算 約分なし③ 分数のわり算 約分なし④ 分数のわり算 約分なし⑤ 分数のわり算 約分なし⑥ 分数のわり算 約分なし⑦ 分数のわり算 約分なし⑧ 分数のわり算 約分なし⑨約分なし ・真分数×真分数の計算ができる。 ・真分数×真分数の計算の仕方や意味が分かる ・数直線や図、言葉の式をかいたり、小数による置き換えや分数を簡単な整数に直して数量関係を明らかにする力を発揮しながら、乗法の意味を確認して、分数×分数の問題を解決していく活動 (学習
002 タイム 分 秒 点/100点 ① 3 3 3 × 3 9 4 5 4 × 5 ② 3 3 3 × 3 9 4 4 4 × 4 16 ③ 3 1 3 × 1 3 4 2 4 × 2 8 ④ 2 1 2 × 1 2 5 3 5 × 3 15 ⑤ 1 11 分数のかけ算 真分数×整数(約分なし) (p4・5) 2 分数のかけ算 真分数×整数(約分あり) (p6・7) 分数のかけ算 仮分数×整数(約分あり) (p9) 5 分数のかけ算 帯分数×整数(約分なし) (p10・11) 3 分数のかけ算 仮分数×整数(約分なし) (p8)分数 ×整数 ,分数 ÷整数 の計算 においては ,整数 の乗除 における 考え方を基礎 として , 被乗 (除)数を分数 に拡張 したときの 式の表している 意味 を理解 できるようにさせたい 。 そのために ,数直線図 や面積図等 で示しながら ,これらを 手がかりに 児童 が自ら計算方法 を




約分なしの分数の掛け算の計算のやり方や意味の教え方は みけねこ小学校
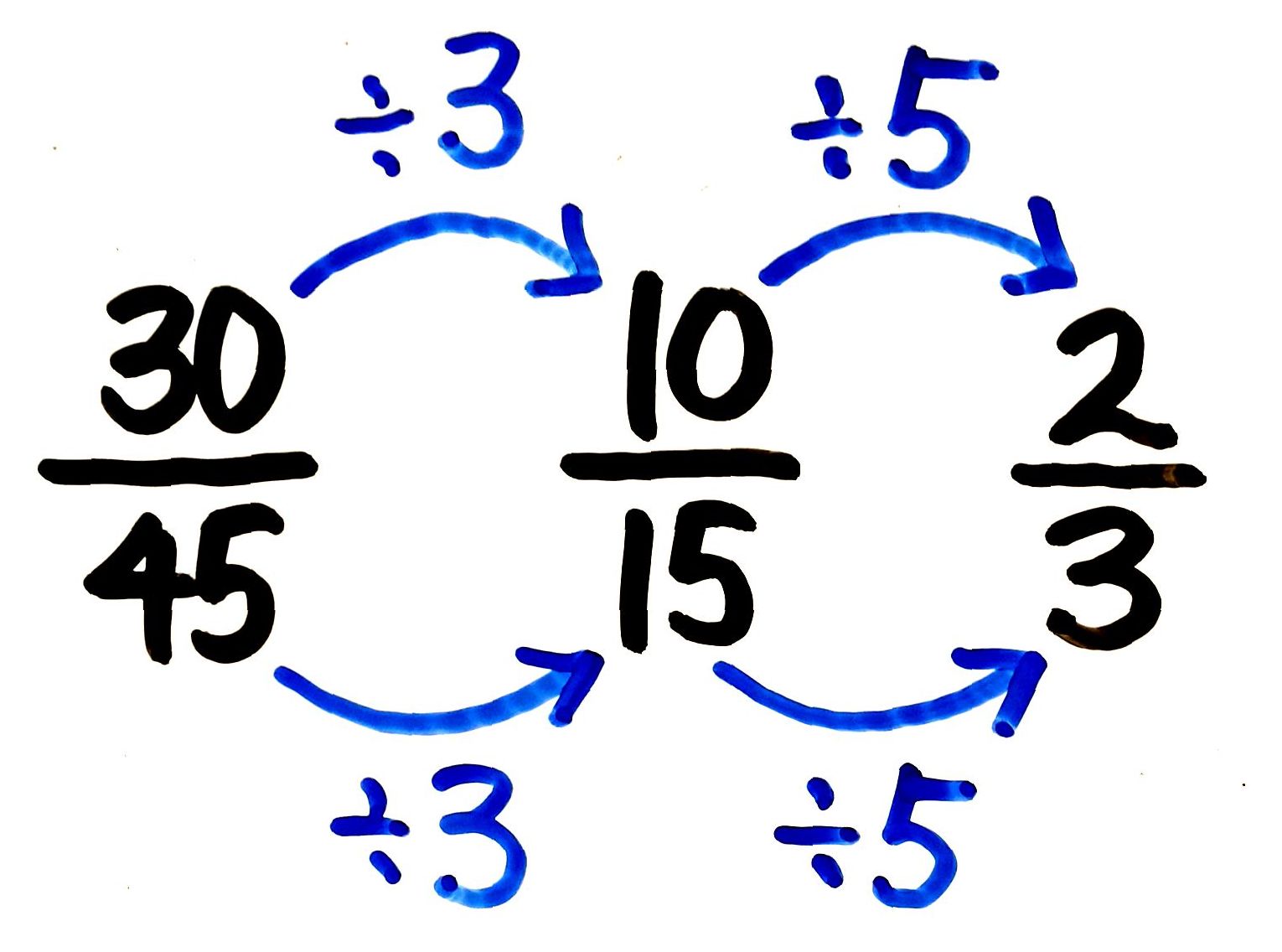



分数の総まとめ 苦手な人でも性質や計算方法を理解できます そうちゃ式 分かりやすい図解算数 別館
③「約分」→次の分数を約分しましょう。 ①分数の掛け算が用いられる場面 ①「~しない~な~。」→ここで約分しない簡単な方法。 ②分数の掛け算の方法(分数×整数) ②「長方形」「縦・横」「広さ」 ①分数の割算が用いられる場面 ①「N等分」→この長方形を2等分すると ②分数の割算Tweet 分数と整数のかけ算の約分のない問題だけを集めた学習プリントです。 整数×分数、分数×整数、どちらの問題もあります。 最初に、図を使って分数のかけ算を具体的に解説してあるので、分数のかけ算を初めて学ぶときに最適です。 また、途中式の立て方もなぞりながらしっかり学ぶことができますので、途中式をうまくかけず計算ミスが増えてしまった・乗数が分数の場合でも乗法の式に表してよいことを理解する。 ・分数×分数の計算のしかたを考える。 ・分数×分数で、計算の途中で約分ができるときの計算のしかたを理解する。 ・整数×分数の計算を分数×分数にしても計算できることを理解する。



Www City Hadano Kanagawa Jp Www Contents Simple A040 Pdf



1
11 分数×分数(約分なし) 41~43 →ⅰプリ11 12 分数×分数(約分あり) 43~44 →ⅰプリ12 13 3つの数のかけ算 45 →ⅰプリ13分数の足し算(分母同じ、繰上なし) 分数の引き算(分母同じ、繰下なし) 単位 長さmm、cm、m、km 重さmg、g、kg;整数×分数の問題と解き方 下記の整数×分数の計算し、できるだけ簡単な形で表してください。 答えを下記に示します。 約分をして、できるだけ簡単な形にしましょう。詳細は下記をご覧ください。 約分とは?1分でわかる意味、やり方、問題、約数、素因
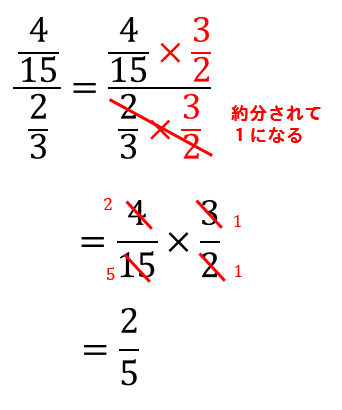



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
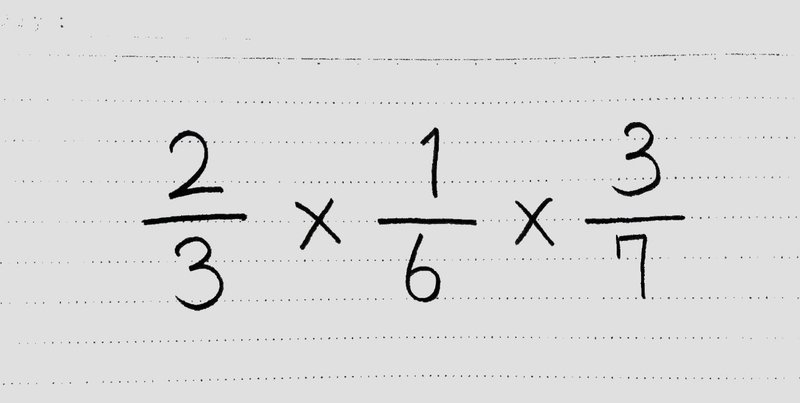



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note
⑨ 3 1 3 × 3 9 5 3 5 × 1 5 ⑩ 1 5 1 × 6 6 5 6 5 × 5 25 分数トレーニング 分数わり算(約分なし) 初回テスト = ÷ = = ÷ = ÷ = = = ÷ = = = = ÷ ÷ = ÷ ÷ = = = = = = ÷ = = ÷ Created Date分数の足し算 分母が同じ1以下の足し算 分数足し算約分なし 分数の足し算・解1まで (分母5まで) 分数の足し算・解1まで (分母9まで) 分数の足し算 (分母6まで) 分数の足し算 (分母9まで) 分数の足し算 (分母2桁1) 分数の足し算 (分母2桁2) ・約分なしの分数の掛け算の計算のやり方や意味の教え方は? 整数を分数にして考えてみる 1つめの考え方は整数を分数に変えて考えると分かりやすくなります。$$(1)3\times \frac{1}{2}$$を元に考察してみます。 まずは3を分数で表してみましょう。
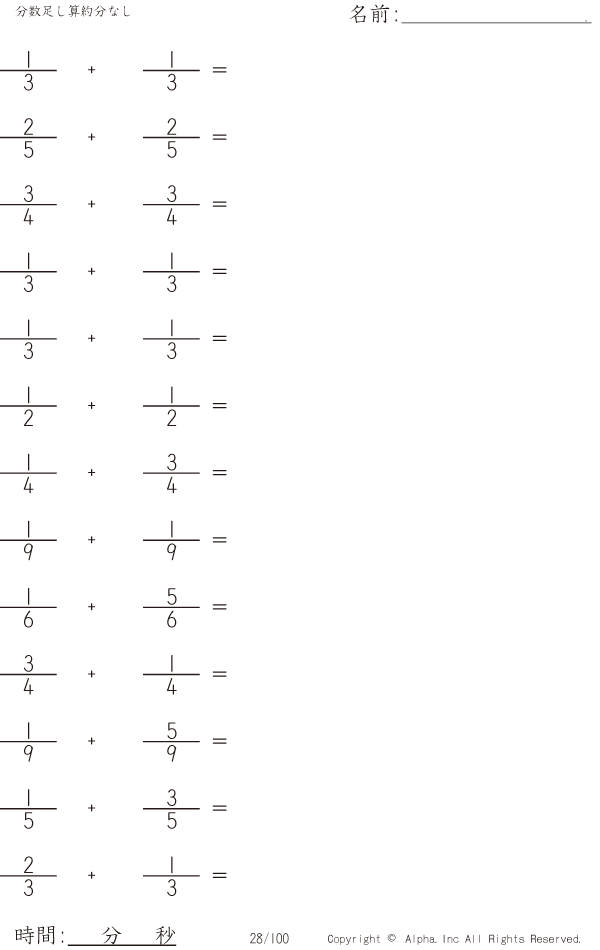



分数足し算約分なし 問題 028 100




すきるまドリル 小学5年生 算数 分数のたし算とひき算 無料学習プリント すきるまドリル 無料学習プリント
③「約分」→次の分数を約分しましょう。 14課 「ぶんすうの かけざん①」 ①分数の掛け算が用いられる場面 ①「~しない~な~。」→ここで約分しない簡単な方法。 (303kb) (262kb) ②分数の掛け算の方法(分数×整数) ②「長方形」「縦・横」「広さ」 15課 「ぶんすうの わりざん①」 ①分数1 単元名 分数×分数,分数÷分数(さらに分数のかけ算わり算を考えよう) 2 指導観 子どもたちは、分数についてこれまでに、端数部分の大きさや等分してできる部分の大きさなど を表すために分数を用いることや同分母の分数の加法・減法、商としての分数の意味、分数と小数 の関係などをツイート 無料ダウンロード・印刷できる、小学6年生の算数プリント分数×分数の計算を繰り返し練習できる問題です。 分数×分数 問題プリント(1) 答え 分数×分数 問題プリント(2) 答え 分数×分数 問題プリント(3) 答え 分数×分数 問題
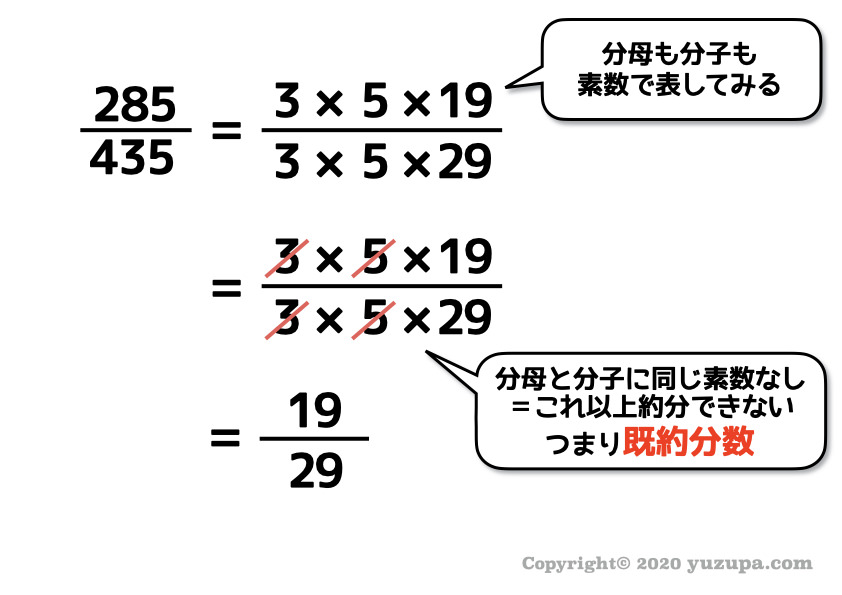



中学入試 問題解説 既約分数を扱う問題 17年駒場東邦 かるび勉強部屋
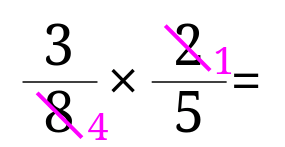



分数のかけ算の約分ができない なぜ斜めでできるの 意味の教え方やコツはどう説明する みけねこ小学校
Tweet 分数×分数で、約分がない問題を集めた問題プリントです。 九九の範囲で計算できる問題なので、無理なく自分で学習できます。 『例題』と『確認』では、分数同士のかけ算の概念を理解するため、図の解説があります。 『仕上げ』と『力だめし』では、分数×整数(整数×分数)の問題も混ぜてあります。 分数×整数(整数×分数)では、約分がある問題も 分数×整数(約分なし) 分数×整数(約分あり) 分数×整数(いろいろな型) 分数のわり算 分数÷整数の計算方法 分数÷整数(約分なし) 分数÷整数(約分あり) 分数÷整数(いろいろな型) 角柱と円柱 角柱の性質 角柱の種類 円柱の性質 角柱と円柱の見取図 角柱と円柱のてん開図 解答About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




くもんのにがてたいじドリル算数 7 小学5年生約分 通分をする分数の計算 本 通販 Amazon




分数ってなぜ比べにくいの 通分の仕方がわかれば分数の計算も簡単に 中学受験ナビ
分数のかけ算1分数と整数の積(約分なし) Author すらぷり Subject 分数のかけ算1分数と整数の積(約分なし) Keywords 分数のかけ算, 算数, 小6, 無料プリント Created001 タイム 分 秒 点/100点 ① 1 1 1 × 1 1 2 3 2 × 3 6 ② 1 1 1 × 1 1 5 5 5 × 5 25 ③ 1 2 1 × 2 2 5 3 5 × 3 15 ④ 1 1 1 × 1 1 5 2 5 × 2 10 ⑤ 2 4
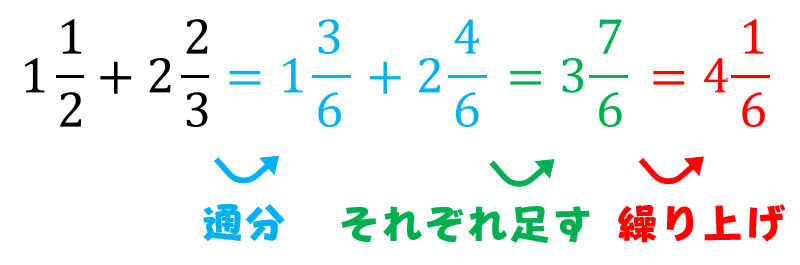



分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




分数のかけ算の計算プリント 真分数編 全450問無料 算数パラダイス




分数のかけ算 分数 分数 無料で使える学習ドリル




算数 分数を通分するときの最小公倍数を簡単に見つける方法を解説 数スタ
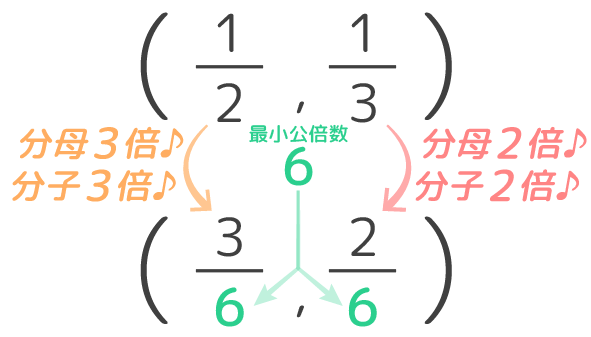



何年生で 分数の通分のやり方教え方と問題演習 3つの分数の通分も そうちゃ式 分かりやすい図解算数 別館




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
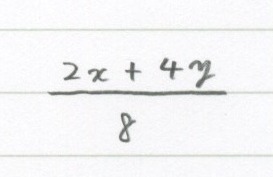



4 2 式の計算 約分の注意点 勉強できようサイト
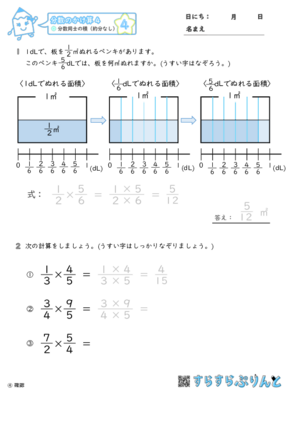



分数のかけ算 分数同士の積 約分なし 小6 学習プリント




約分ってなに Youtube




通分と約分 算数用語集
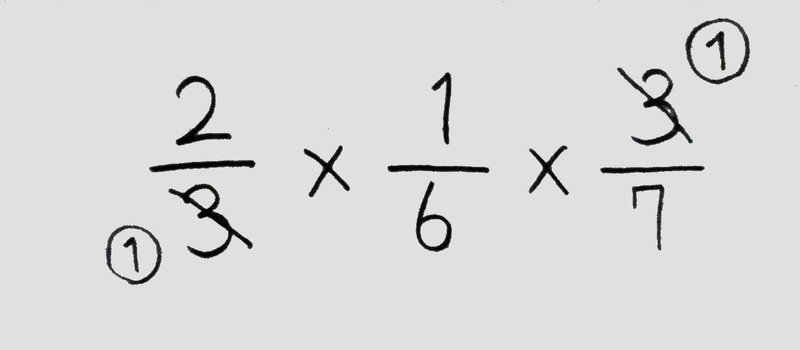



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note




画像 教師 小学校3年生は分数の約分禁止 不満があるなら他のクラス行け Himohimomatomeのblog
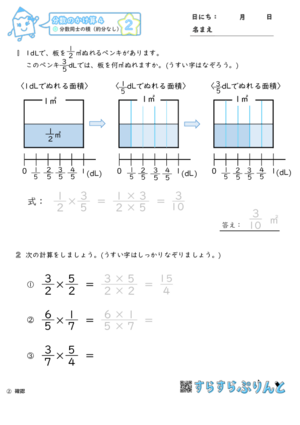



分数のかけ算 分数同士の積 約分なし 小6 学習プリント



根号計算 約分
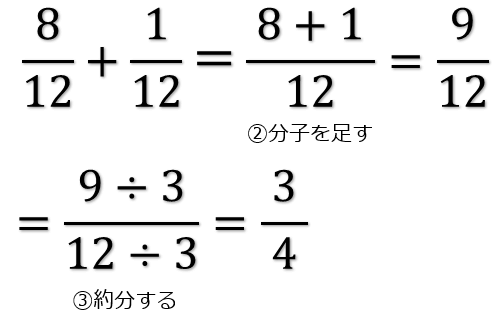



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数の足し算で 約分 が発生する条件 Tsujimotterのノートブック
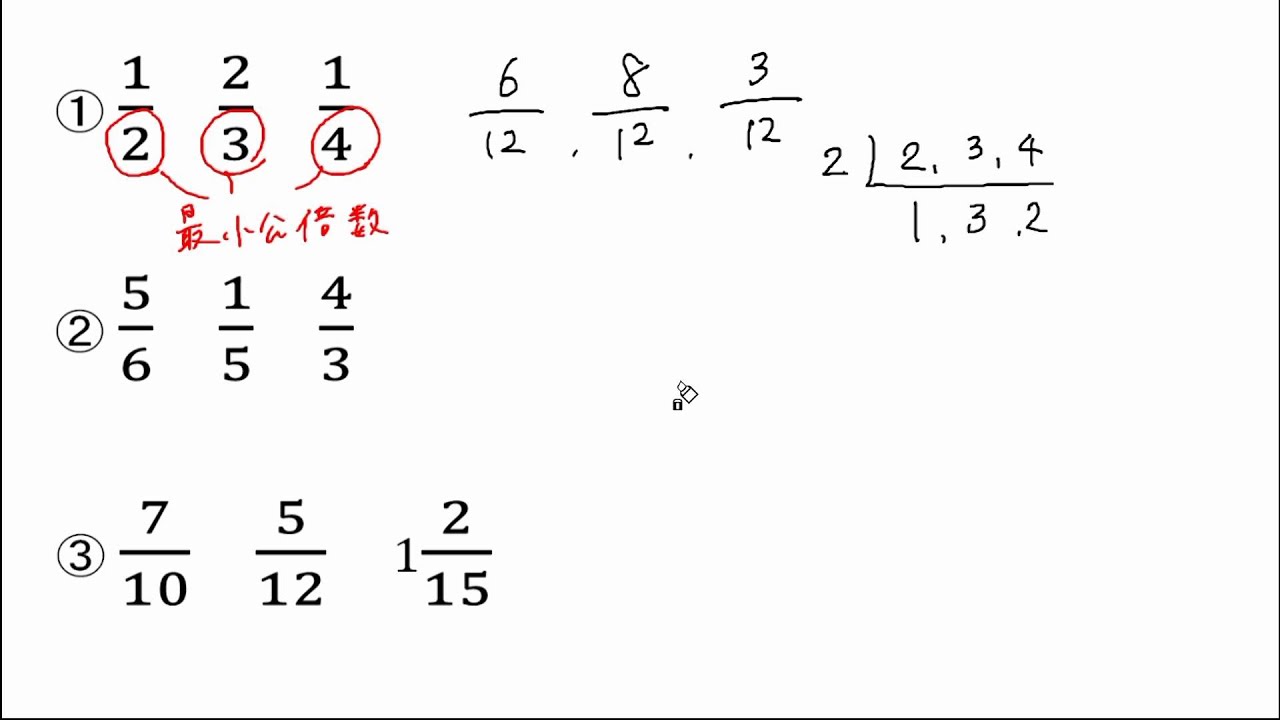



通分 問題練習 Youtube
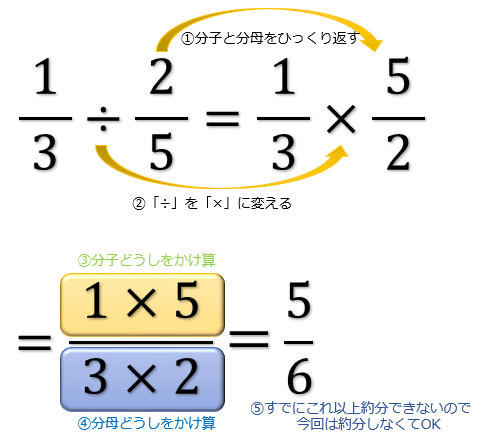



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



約分 通分のポイント



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料




かみのドリル 約分と倍分
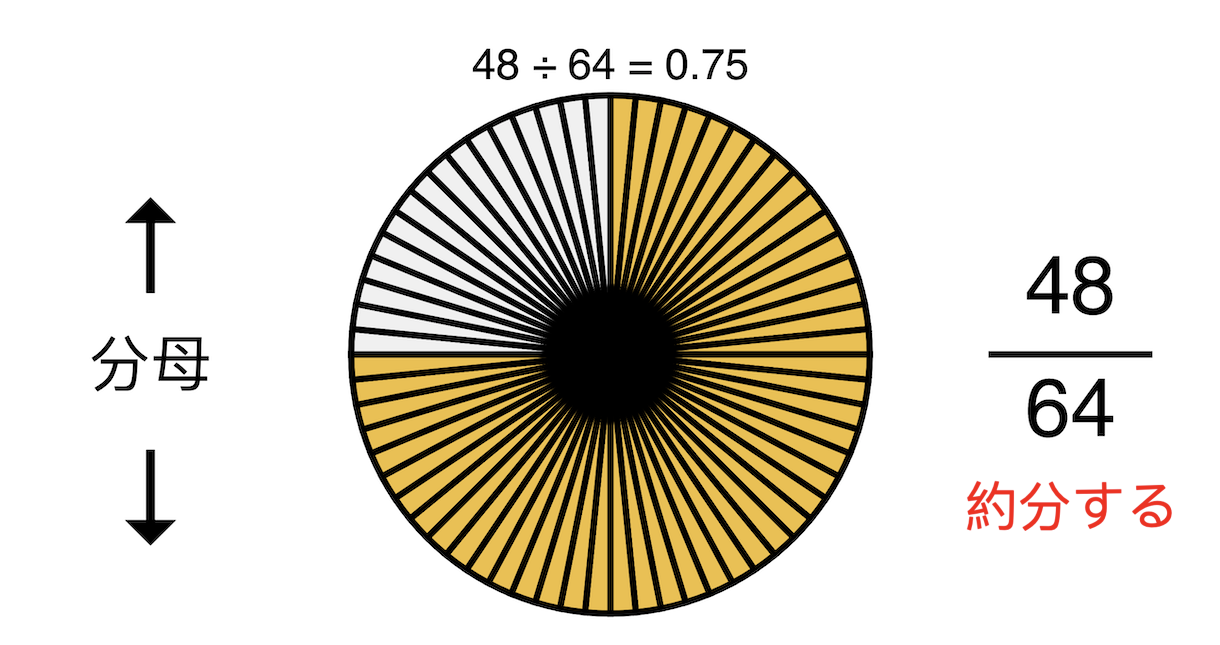



分数で遊ぼう 自学をサポートする教材アプリ Jigaku シリーズ Jigaku Js 福野泰介の一日一創 Create Every Day By Taisuke Fukuno



通分のやり方 大人の学び直し算数 計算のやり方解説 無料
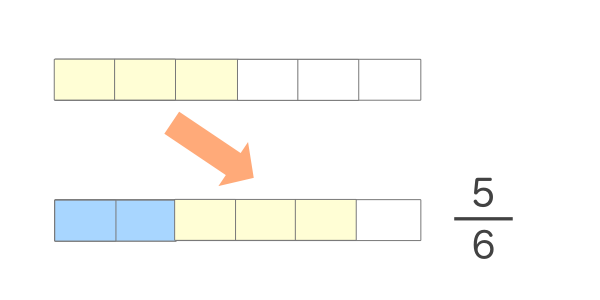



分数の足し算 簡単に計算できる電卓サイト



5年生の 分数 整数 の4本目のソフトを開発中 さくら社
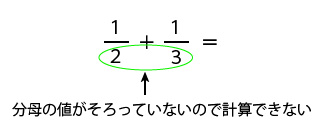



通分と約分 もう一度やり直しの算数 数学
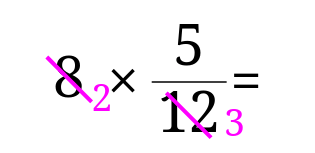



分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校




分数の足し算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun




分数の足し算や引き算の問題 通分できるかが非常に大切 中学や高校の数学の計算問題




小学5年生の算数 分数の約分 通分 練習問題プリント ちびむすドリル 小学生




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料
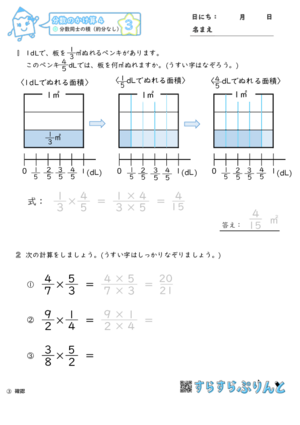



分数のかけ算 分数同士の積 約分なし 小6 学習プリント




帯分数の足し算 通分あり Youtube
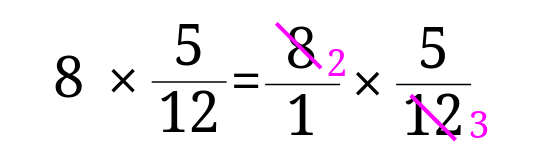



分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校




算数 分数の足し算 Youtube
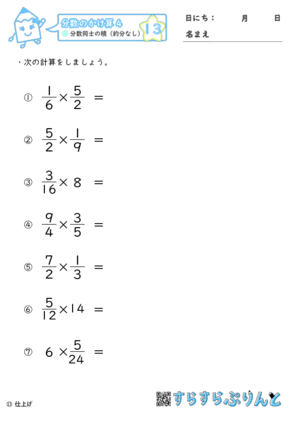



分数のかけ算 分数同士の積 約分なし 小6 学習プリント



1
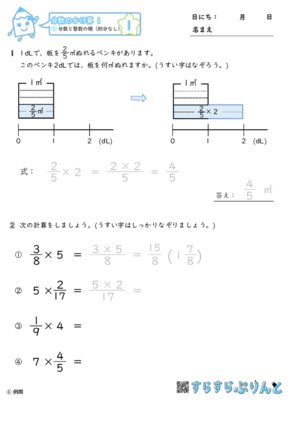



分数のかけ算 分数と整数の積 約分なし 小6 学習プリント
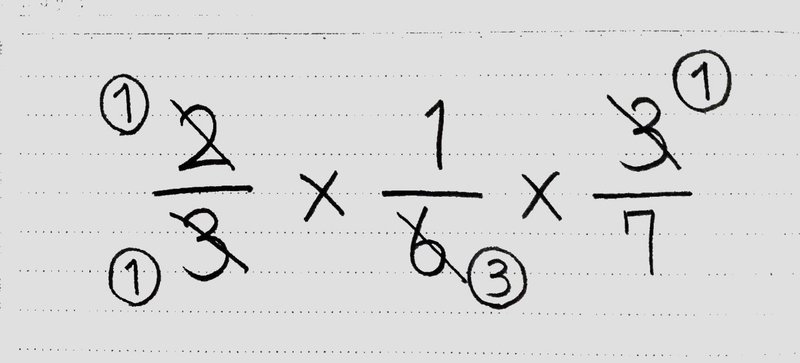



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note




小学5年生の算数 異分母の分数の足し算 練習問題プリント ちびむすドリル 小学生



1




小学3年生 算数ドリル 分数2 分母が同じどうしのたし算 プラス パル




分数のかけ算 式の中で約分する Youtube
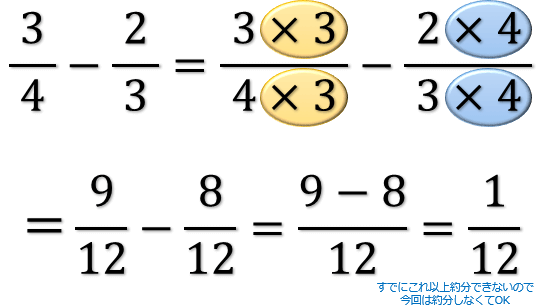



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




小学校5年 算数 分数のわり算2 約分のあるわり算 Youtube




小学6年生 算数 無料問題集 分数 分数の約分の無い掛け算 おかわりドリル
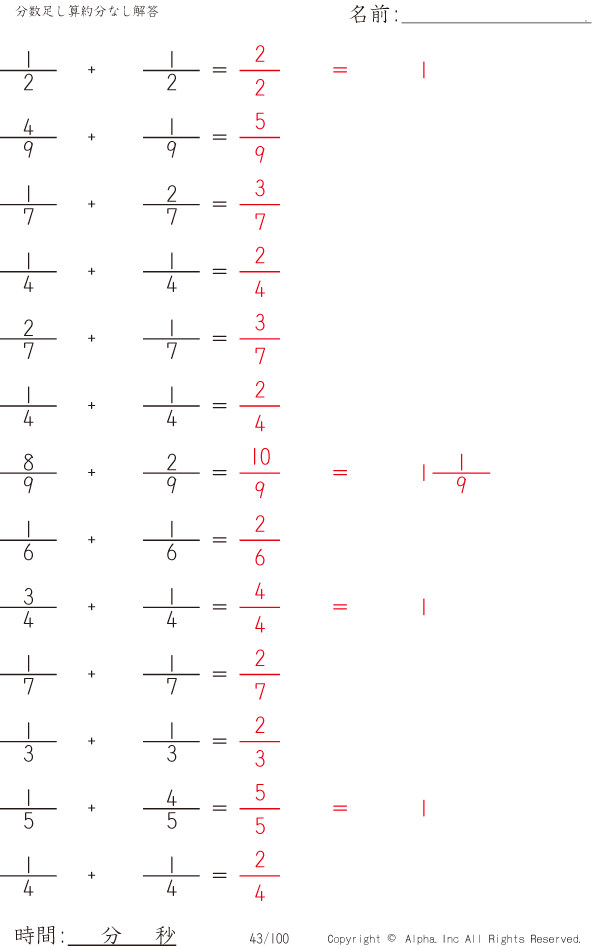



分数足し算約分なし 解答 043 100




小学生算数計算プリント ポッ プりんと




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




数基礎 Com 帯分数のかけ算が分かる方法




分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校



算数4年から6年



Www Kumonshuppan Com Wpr Pdf Parts Pdf




約分がない整数と分数の掛け算の教え方は どうやって考えるといいの みけねこ小学校
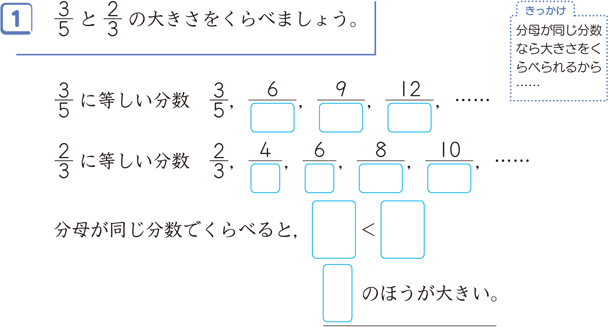



通分と約分 算数用語集




小学5年生向け分数の引き算計計算



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料
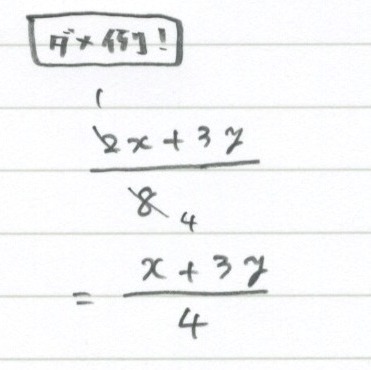



4 2 式の計算 約分の注意点 勉強できようサイト
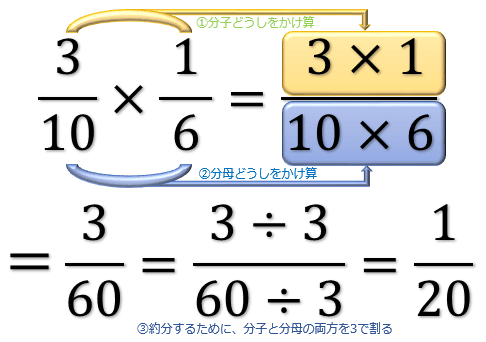



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




Telecharger 分数 割り算 問題 分数 掛け算 割り算 混合 問題
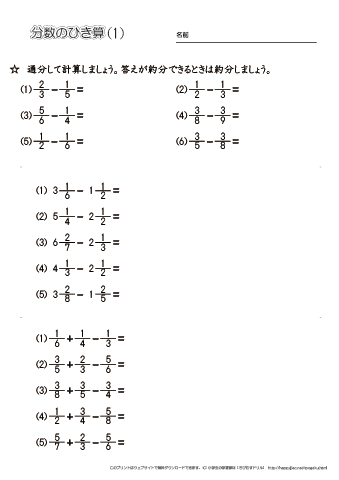



小学5年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生




小学6年生 算数 無料問題集 分数 分数の約分の無い掛け算 おかわりドリル




小学6年生の算数 分数のかけ算 分数 整数 分数 分数 練習問題プリント ちびむすドリル 小学生




分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun
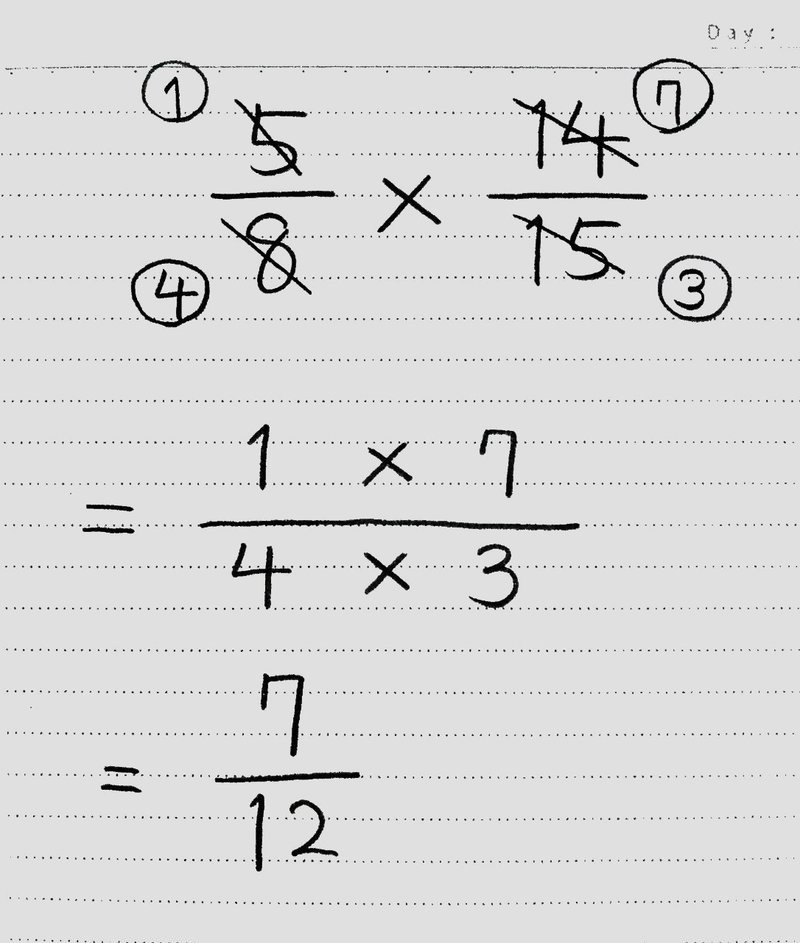



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note




分数の分子に足し算がある場合 約分が出来ないのはなぜですか 分子 数学 教えて Goo




通分の新着記事 アメーバブログ アメブロ




算数 分数の約分のしかた 教え方のコツ なるほど 塾講師が教える教え方のコツ




分数のかけ算 分数同士の積 約分なし 小6 学習プリント
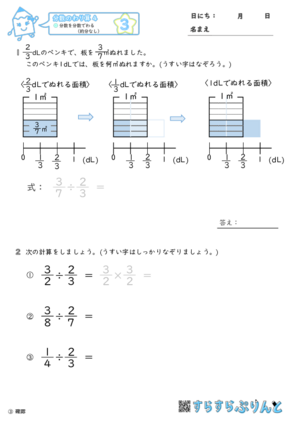



分数のわり算 分数を分数でわる 約分なし 小学6年算数




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




分数の大小関係 通分や小数にするのが解き方のコツだ 中学や高校の数学の計算問題




分数の割り算の計算プリント 帯分数編 全180問無料 算数パラダイス
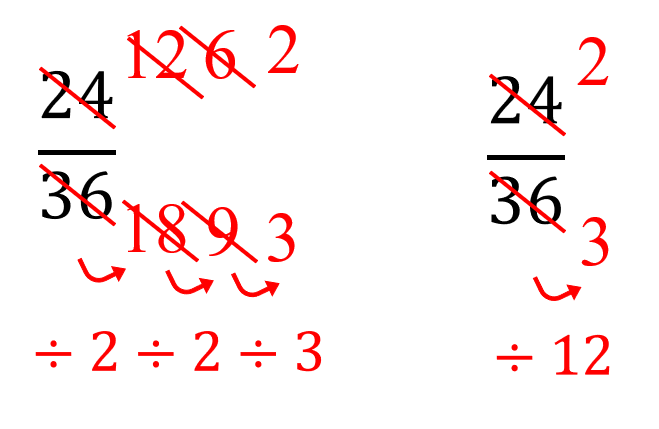



分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス
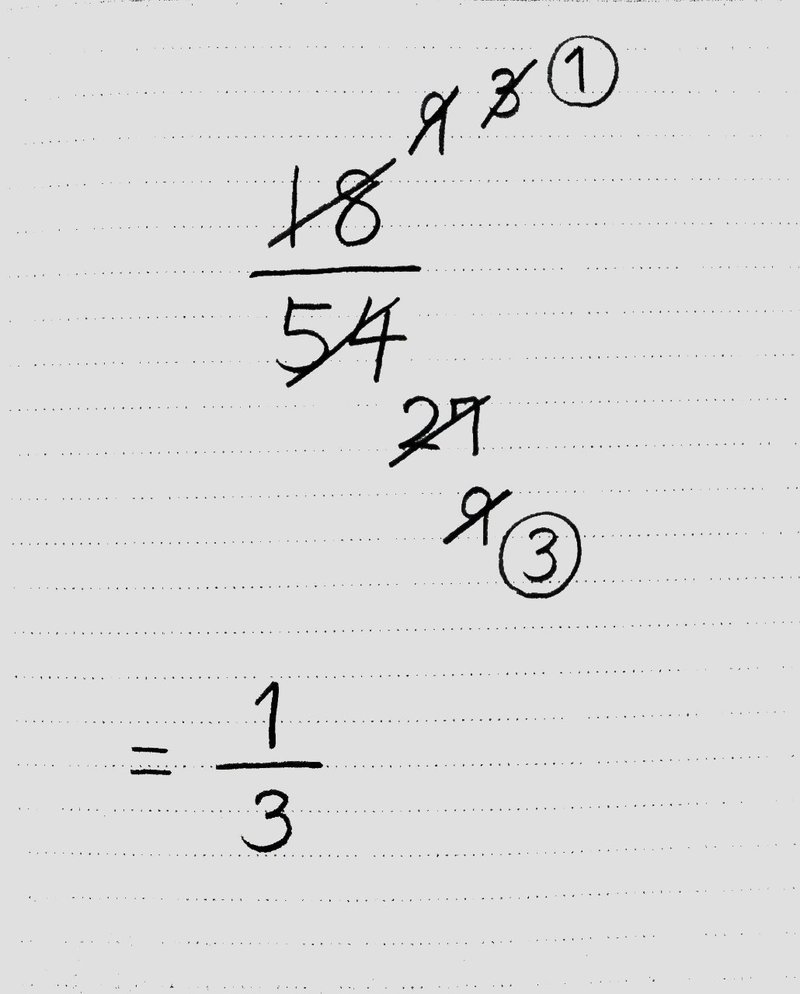



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note




分数の約分を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




分数の約分の練習問題 計算ドリル 問題集 数学fun



2




分数のわり算 分数を分数でわる 約分なし 小学6年算数
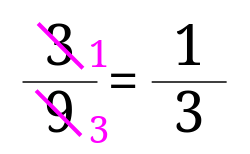



約分が苦手で分数の計算が分からない 分かりやすく意味や理由 コツを理解させる教え方のポイントとは みけねこ小学校
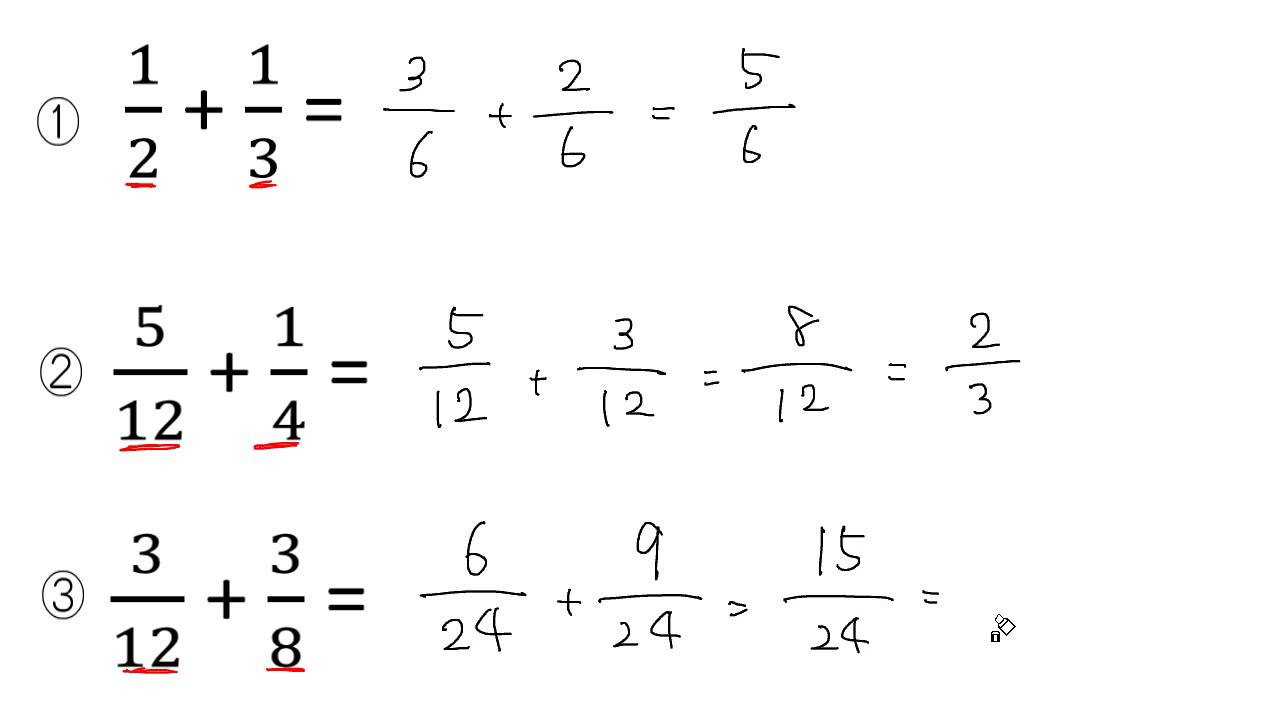



分数の足し算 引き算 通分あり Youtube
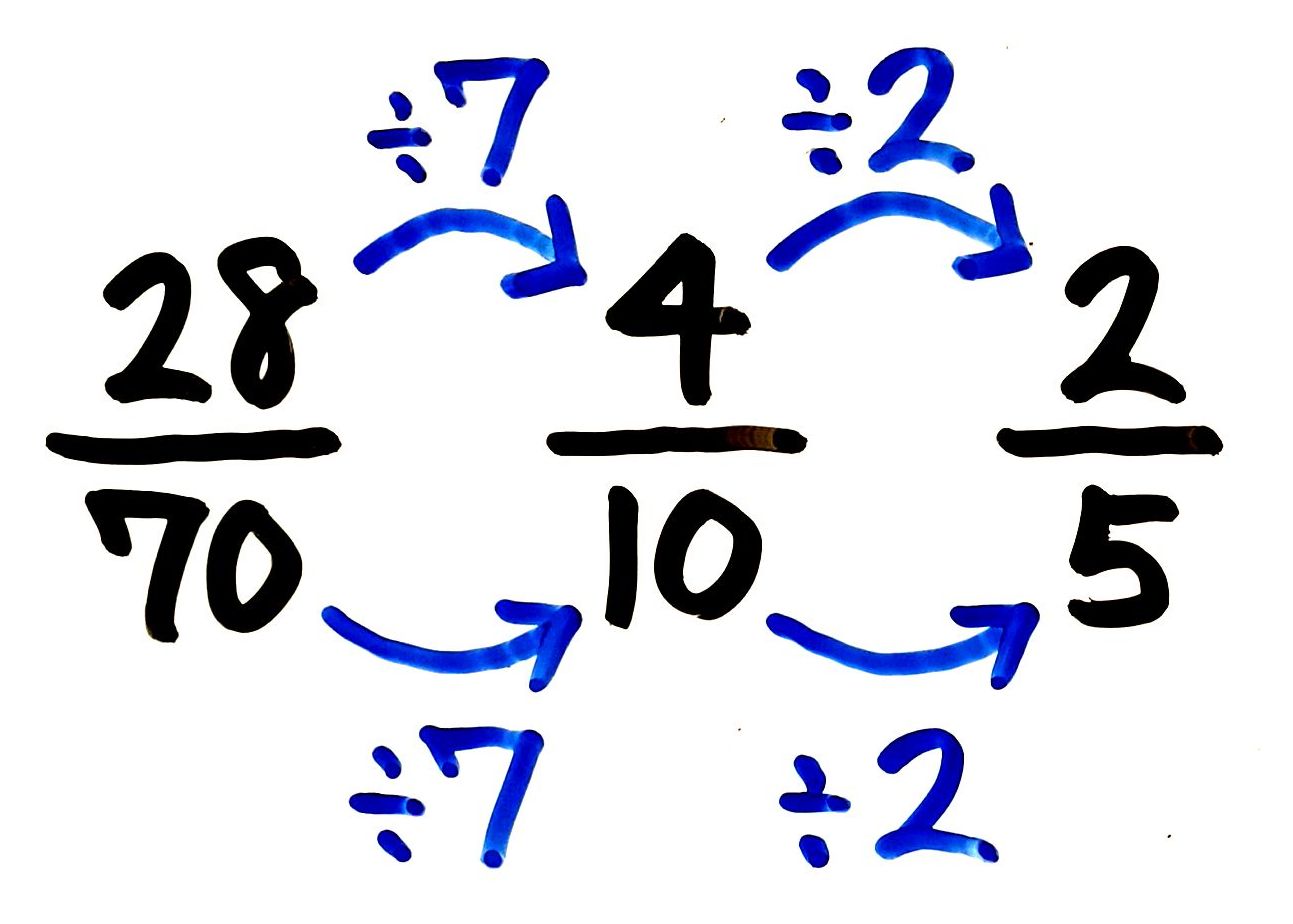



既約分数のテクニック 解き方は2つでok 中学受験 塾なし の勉強法




小5 約分 約分の仕方 日本語版 Youtube



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料



1




分数の足し算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス



算数4年から6年




小学生の算数 分数計算のプリント置き場 受験経験ゼロ それでも娘の中学受験を本気で応援する日記


