3次方程式の解の公式とその証明、さらには3次方程式が発表されるまでの経緯について紹介します。 ①歴史 ②解の公式と証明 ③例 ①歴史 1545年、ジェロラモ・カルダノが著書『アルス・2次方程式の解の公式(虚数解含む) 3次方程式 フリ-ソフトwxMaximaによる高次,連立方程式の解き方 ===二次方程式の解き方=== (因数分解による方法) 解説 ≪原理≫ AB =0 ならば A =0 または B =0 ↑ 2つのものを掛けて0になるときは,どちらかが0だと現在地 と前後の項目 ※ 3次以上の式の因数分解を行う強力な方法として「因数定理」があるが,これは数学IIで習う.数学Iではもっと簡単に「因数分解公式」「置き換え」などで因数分解できるものだけを扱う. 証明するには右辺を展開してみるとよい

因式分解三次方
3次方程式 因数分解 公式
3次方程式 因数分解 公式-ここでは、3次の乗法公式や因数分解について学びます。 学習のポイント 1(a+b) 2 と(a-b) 2 の復習 2(a+b) 3 と(a-b) 3 との展開 3乗法公式3x2 6x = 24 3 x 2 6 x = 24 3x2 6x− 24 = 0 3 x 2 6 x − 24 = 0 左辺の全ての項は3で割り切れるので割ったら簡単な形になります。 x2 2x− 8 = 0 x 2 2 x − 8 = 0 手順②より、因数分解します。 (x 4)(x− 2)=0 ( x 4) ( x − 2) = 0 乗法公式 の基本形を利用した因数分解です。 手順③。 「x 4 = 0 x 4 = 0 」 、または 「x− 2 = 0 x − 2 = 0 」 のときにときに等式は成り立つので、解




ベスト 因数分解公式中学 ニスヌーピー壁紙
三次方程式を解く問題では、まず因数分解の公式に当てはまらないかを確認します。 この問題は「\(a^3 − b^3 = (a − b)(a^2 ab b^2)\)」で因数分解できそうですね。三次方程式の解 助かりました。 解の候補にd/aを持つことを忘れていていました。 ELISAのスタンダード曲線の3次式から標本の値を算出するのに利用しました。 自分でもプログラムを組みましたが,こちらの計算と答えが同じだったので,結果に自信が持てました。 実数解がグラフィカルに表示される点もよかったです。 三次方程式の解を出すプログラムを作成 x^2=X x2 = X とおくことによって
3次の乗法公式と因数分解 (1) オープニング(1分46秒) (a+b)2 と (ab)2 の展開の復習(5分14秒) (a+b)3 と (ab)3 の展開(7分14秒) 乗法公式(4分22秒)12 2次方程式,3次 を用いて根を求める公式(カルダノの公式,前の講演参照)が知られています.それでは4次 あるいは,より高次の場合はどうなるかという問題に対する一つの答えが,次の代数学の基本 定理です. 13 定理(代数学の基本定理) 複素数係数のn次方程式 xn a n 1x n 1 a n 2x n 2このページでは、 数学Ⅱの「3次方程式の解き方」についてまとめています。 3次方程式の解き方は、因数分解、置換、組立除法の3パターンあります。 それぞれの公式や計算方法を,具体的に問題を解きながらわかりやすく解説していきます。 組立除法のやり方は「組立除法 やり方と計算」で
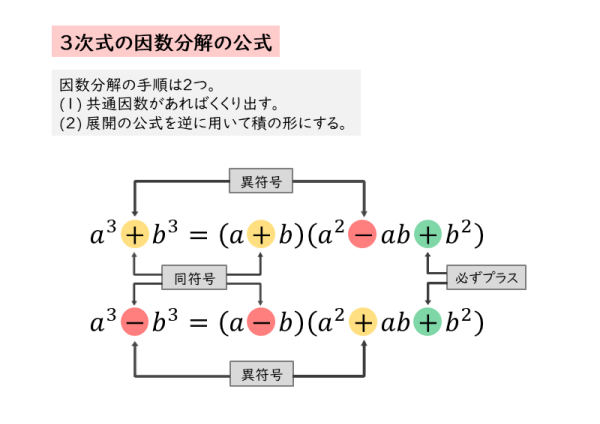
因数分解の手順は、次のように行う。 ① 共通因数がある場合は早く、かっこでくくり出す。 ② 因数分解の公式が適用できるかどうかを調べる。 ③ 公式がすぐ適用できない場合は、少し工夫して式を変形し、整理し因数分解できる形にする。応用分野: 放物線の定積分, 式の展開と因数分解, 因数分解の手順, 因数分解 (x^2x1)(x^2x1), 因数分解, 問題リスト ←このページに関連している問題です三次多项式一定能因式分解得出实数解,因为每个三次项都一定有个实根。 三次方多项式如x 3 x 1含有无理实根,不能被因式分解成含有整数或有理数系数的多项式。




解三次方程式的三個根 Youtube



1
3次式の因数分解3次式を因数分解するとき、公式の適用をまず考えます。公式が適用できないとき、因数定理を用います。例題1有理数の範囲で、\(x^37x6\) を因数分解しなさい。解説公式で因数分解できないので、因数定理を使います。\(P(x)=x^37x6\) とおきます。 \(x^37x6=(xk)Q(x)\) と因数分解されるので、このような \(k\) を因数定理で探します。\(P(k)=0\) を満次の方程式解け。 (1) (2) ① 高次方程式は因数分解しないと解けません。 ② 因数分解は、解の 1 つ を見つけて、因数定理によって を因数にもつことを 用いて下さい。実際の計算には、筆算もよいのですが、組立除法を用いると簡単 ですね。2次式が因数分解できないときは、解の公式を用いて 解の公式をマスター 二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 本記事では「二次方程式とは何か」という説明から、3つの解き方の使い分けまでを解説します。 もし、上の3つの二次方程式の解き方を使 55 akk




因式分解x六次方 64y六次方 12x平方y平方 1 雨露学习互助
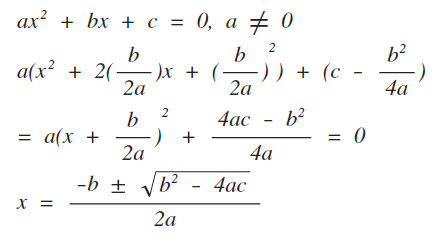



高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
正の数と負の数 22 文字と式(中学) 19 一次方程式 23 比例と反比例(中学) 16 平面図形(中学) 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9 式の計算 30 二項定理 14 等式と不3次方程式 x^3y^3z^33xyz=0を考える 本記事では三次方程式の"一般的な解き方"を紹介します。 よく有名なのはカルダノ・タルタリアの方法ですが、実は以下の方程式を考えることで 解くことができます(もちろん解の公式も導出できます) 今日の主役は 3次方程式を解くとは、因数分解して、 (XA) (XB) (XC) = 0 とする事であり、 この時、3次方程式の解はX=A, B, Cとなる。 (二次方程式を因数分解して解くのと考え方は同じ)




3次以上の展開と因数分解はどうなる 公式の総まとめ




多项式除法 维基百科 自由的百科全书
★二次方程式★ ③ 解の公式を使って解く これまで①平方根を使う解き方と②因数分解を使う解き方をやってきました。 ところが、平方根も使えない、因数分解も使えない形の二次方程式が出てきます。 例えばこんなの! 高次方程式を解くためには因数分解が必要ですが、いつも公式に当てはまるとは限りません。 因数定理は、因数分解の公式が使えない場合でも 最初の因数を見つける ことができます。 それでは、因数定理を使って例題を解いてみましょう。 21 3次式の因数分解 のときもやり方は同じです。 やり方がわかったら、実際に問題を解いてみましょう。 次の式を因数分解せよ。 3 まとめ 以上が、『展開・因数分解の公式一覧』です。 この単元の公式を、PDFファイルでプリント1枚にまとめました




三次方程式公式三次方程式求解公式 Pripdw




高中数学三次分解因式 高中数学如何求解一元三次方程 如何因式分解 三人行教育网 Www 3rxing Org
根の公式とは 上: 3次方程式 前: ある三次式の因数分解 根と解 南海 方程式の問題を考えるので,まず「方程式の解」についてまとめておく. 教科書にはどのように書かれているかな. 2乗の場合も、 基本展開の公式 と 基本因数分解 で見たように、展開で出てきた公式が因数分解の公式にもなっていましたね。 3乗の場合も同じで、 基本三次式の展開 の左辺と右辺を入れ替えたものが、因数分解の式となります。 解法を聞いたカルダノが勝手に自著で発表したとされる \\1zh 2次方程式の解の公式は,\ 紀元前からすでに知られていた \\2zh 16世紀になってようやく3次方程式の解の公式を発見した数学者達だが,\ 1つの困難に直面する \\2zh x^315x4=0の解を求めるとしよう \\2zh 因数定理を用いると,\ (x4)(x




因式分解 整式的乘除与因式分解ppt课件2 Ppt课件下载 人人ppt




三次方程式公式三次方程式求解公式 Pripdw
4 次多項式の3 次分解式 g(t) = q24(2tp)(t2r) :3 次分解式(解核多項式, resolvent) T = 2t とおいて、 R(T) = g (T 2) = T3pT 24rT (q 4pr) R(T) が因数分解できる f(X) の根が3 乗根を用いずに表せる 数の世界 17 α, β \alpha,\beta α,β であるとき, a x 2 b x c = a ( x − α) ( x − β) ax^2bxc=a (x\alpha) (x\beta) ax2 bxc = a(x −α)(x− β) と因数分解できる という性質(※)を使うと, 3 x 2 − 10 x 8 = 3 ( x − 2) ( x − 4 3) = ( x − 2) ( 3 x − 4) 3x^210x8\\ =3 (x2) (x\frac {4} {3})\\ = (x2) (3x4) 3x2 −10x 8 = 3(x−2)(x − 34




四次方程 维基百科 自由的百科全书




3次式の因数分解 公式とやり方について問題を使って解説 数スタ



因式分解三次方



因式分解三次方




一元二次方程怎么解 解一元二次方程的基本方法 三问网



列竖式进行因式分解 知乎




因式分解技巧 二元二次的分解 星空暗流 博客园




高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト



X3次方 Y3次方 怎么因式分解还有因式分解的思路 作业 慧海网




3次方程式の解の公式の証明 省略なし 怜悧玲瓏 高校数学を天空から俯瞰する




二元二次方程的解法 知乎




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
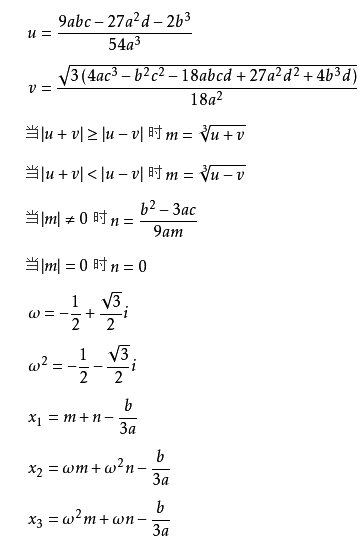



一元三次方程快速解法 快资讯



考研数学 十分钟掌握求解一元三次方程的四种解法 公式法 因式分解法 待定系数法 长除法 及使用背景 哔哩哔哩 Bilibili



高二数学实系数一元二次方程教案 莲山课件




高校数学 因数分解公式と3次式の因数分解 受験の月




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




因式分解之待定係數法 一元三次多項式分解 每日頭條




分解因式方程的公式 三次方分解因式方法 三人行教育网 Www 3rxing Org




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




数学技巧 一元三次方程求解 十字交叉法解一元三次方程 个人高中偶然发现的一个数学技巧 知乎
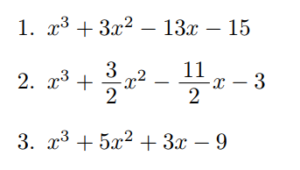



因数定理を利用した因数分解の練習問題 高校数学の知識庫




三次方程式の解き方とは 因数分解や解の公式を例題付きで解説 高校生向け受験応援メディア 受験のミカタ



一元三次方程的图像 万图壁纸网



一元三次方程怎么解 高三网




剖析一元二次方程的3种解法 你的时间很宝贵 就选最快的 每日头条



三次因式分解 3次方多项式有什么因式分解的方法举些例子 尚书坊




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




三次函數因式分解計算器factoring Cubic Function Calculator 學校沒有教的數學 學校沒有教的數學




十字相乘法因式分解解一元二次方程 知乎




因式分解三次方



初中数学解一元四次方程 看似有难度 其实通过换元降次就很简单 哔哩哔哩 Bilibili
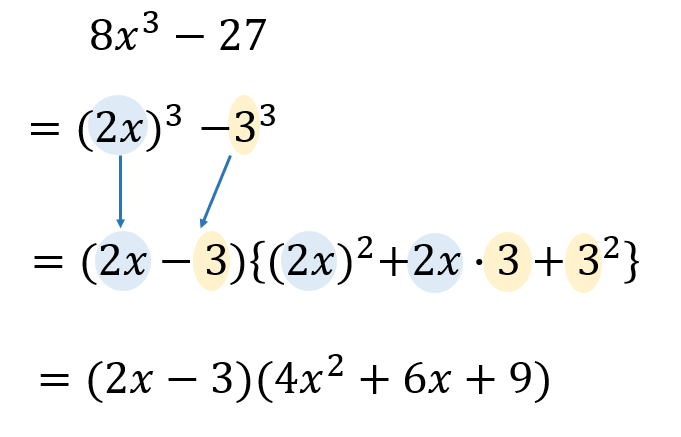



3次式の因数分解 公式とやり方について問題を使って解説 数スタ




因式分解经典解析 人人焦点




高校数学 数 11 因数分解 3次式の公式編 Youtube



1




因式分解练习题 因式分解试根 环球信息网




6种方法来因式分解二次多项式 二次方程




因式分解 多项式优美的舞蹈 雪花新闻




ベスト 因数分解公式中学 ニスヌーピー壁紙



Http Mail Knu Edu Tw Syokou Calculus Ch1 4 Pdf



解方程 X 27x 54 0 立方和公式因式分解解题 哔哩哔哩 Bilibili



初中数学因式分解常用解法有哪些



高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium




一元三次方程发展史及解法解读 每日头条




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す




三次方 三次方程式展開



06一元二次方程的解法 三 公式法 因式分解法 知识讲解 提高 K12资源




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ




解一元三次方程 搜狗百科




如何因式分解三次多项式 12 步骤




一元三次多项式因式分解的两种方法 Longlongqin的博客 程序员宅基地 一元三次因式分解 程序员宅基地



一元三次方程的图像 万图壁纸网




因式分解三次方



1



高校数学 3次方程式 解き方一覧 因数分解 置換 組立除法 学校よりわかりやすいサイト
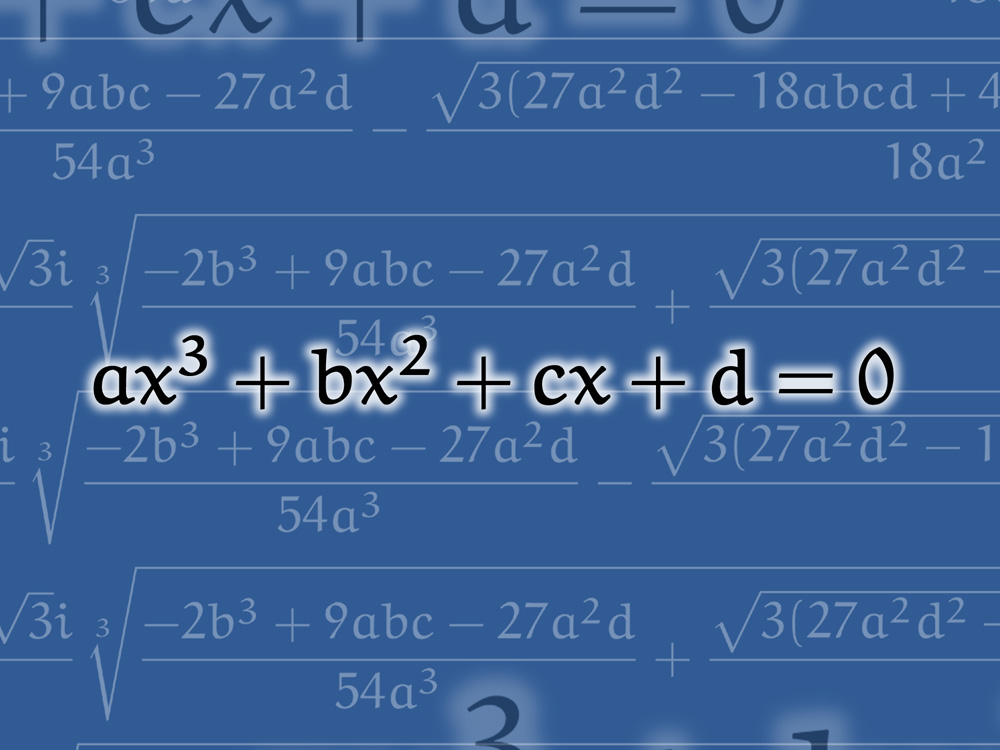



3次方程式の解の公式 カルダノの公式 大島学習塾のホームページ
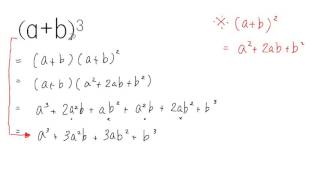



2 三次方程式展開



ある三次式の因数分解




三次方程 三次方程的英文名是cubic Equation 指的是一種數學 百科知識中文網
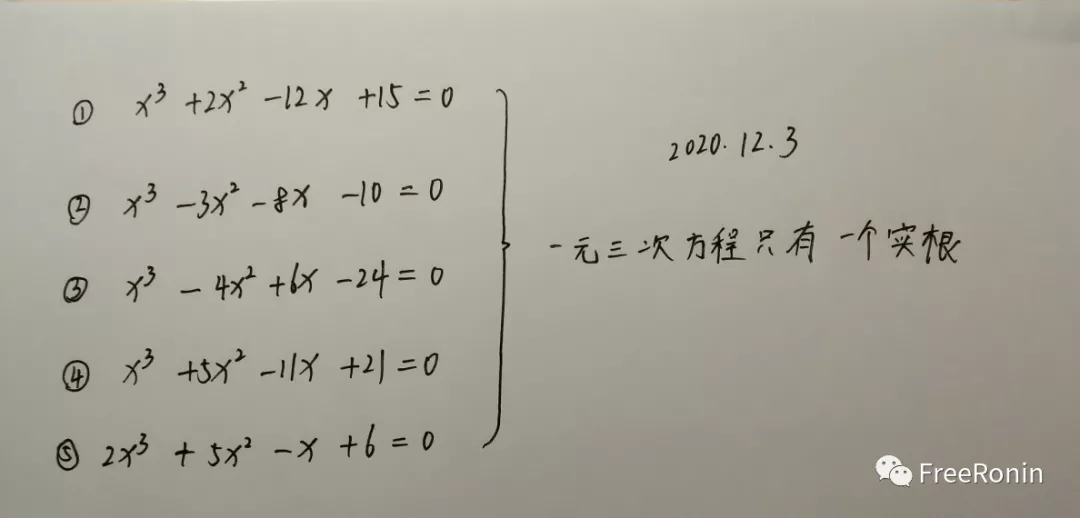



数学技巧 一元三次方程求解 十字交叉法解一元三次方程 个人高中偶然发现的一个数学技巧 知乎




一元四次多项式配方 一元三次多项式怎么进行因式分解 三人行教育网 Www 3rxing Org




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium



解多次函数 三次函数怎么因式分解 函数查询



二三事 一元二次方程式 Morpheusyk The Simplexity 痞客邦



三次方程化简公式 西瓜视频搜索




一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 雪花新闻



06一元二次方程的解法 三 公式法 因式分解法 巩固练习 提高 K12资源




三次项因式分解三次方分解因式方法
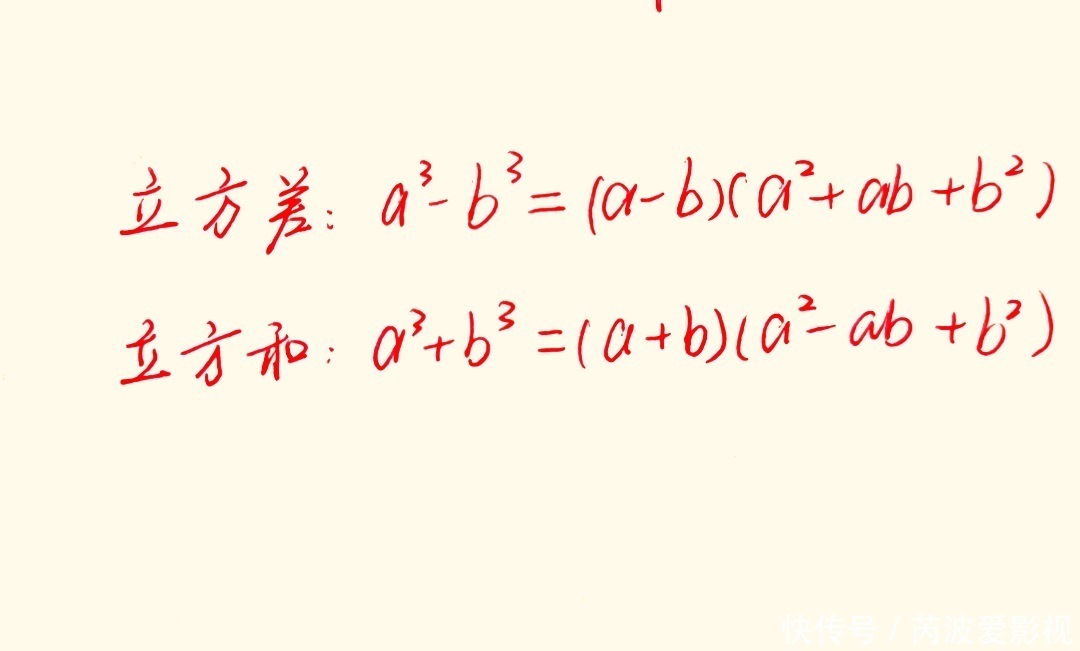



因式分解x3




三次方程式展開 三次方程式の解の公式 Rtndn




3次式の因数分解 公式とやり方について問題を使って解説 Youtube
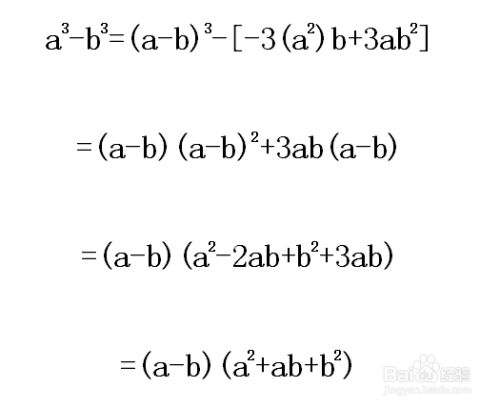



X的三次方减一怎么因式分解 百度经验



數學第三冊 因式分解解一元二次方程式 教育學習中心 痞客邦




一般三次方程式的解 配立方 Youtube




三次方程式の解き方とは 因数分解や解の公式を例題付きで解説 高校生向け受験応援メディア 受験のミカタ



完了しました 因数分解3 次 ニスヌーピー壁紙



因式分解练习 不要墨守成规 数学的特点就是变通 方法




一道高考数学题 一元三次方程求解 X 3x 2 0 网易订阅




一元二次方程求根公式
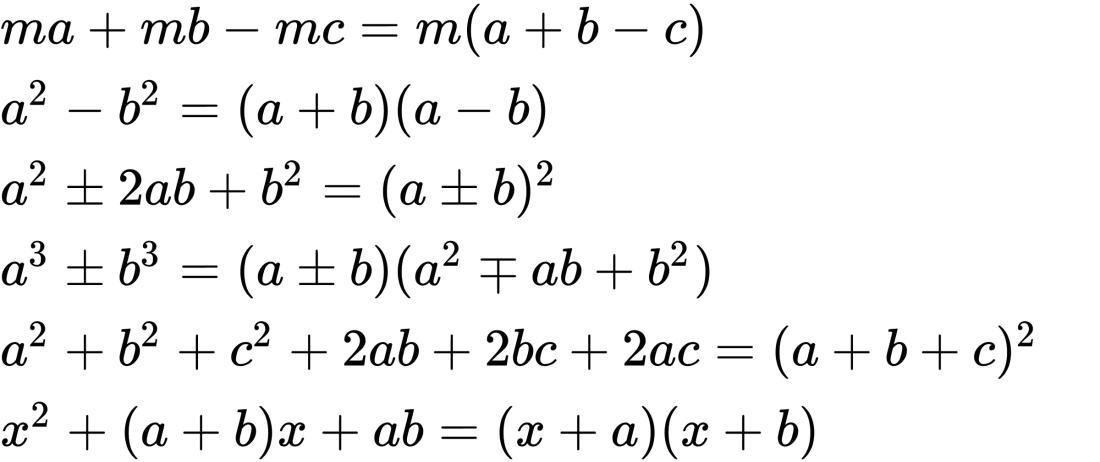



因式分解公式方法 搜狗搜索




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




2 二元三次方程式




2 3b觀念01因式分解三次多項式 為什麼我們需要牛頓定理 Youtube




一元三次方程怎么配方 快资讯




八年级数学下册一元二次方程一元二次方程的解法因式分解法练习新版沪科版下载 Word模板 爱问共享资料




三次方程式公式三次方程式求解公式 Pripdw




一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 系数



因式分解三次方




因式分解三次方



1




求一元二次方程的根的公式




解一元二次方程式 因式分解法 十字交乘法 Youtube



一元二次方程的解法 公式法 因式分解法和十字相乘


